Proof that Out of 6 Persons Either 3 are Friends or 3 are Strangers
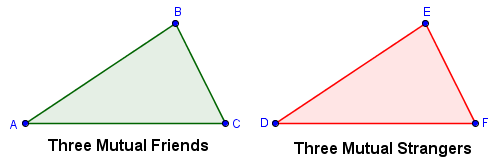
Did you know that out of 6 people, either 3 are friends or 3 are strangers? Three are friends in the question means mutual friends: A and B are friends, B and C are friends, and A and C are friends. Three are strangers also mean that out of three persons, none of whom know each other.
In the mathematical proof below, we represent the individuals by vertices and the relationships by edges. As we can see, we can form triangles. In the triangles below, a green edge connecting two vertices means that the persons represented by two vertices are friends and a red edge connecting two vertices means that the persons represented by two vertices are strangers. A triangle formed by edges of the same color represents three mutual friends or three mutual strangers. We highlight this relationship by filling the interior of the triangle with the appropriate color.
The Proof
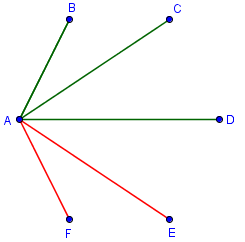
Suppose A is meeting B, C, D, E and F. Now, each of the five persons is either a friend or a stranger to A. This means that in the representation, each edge connecting A and any of the 5 persons is either green or red. Notice that if we make these connections, at least three are red (red ≥ 3) or at least three are green (green≥ 3) as shown in the table.
| Green | Red | green ≥ 3? red ≥ 3? |
| 5 | 0 | Yes, 5 ≥ 3 for green |
| 4 | 1 | Yes, 4 ≥ 3 for green |
| 3 | 2 | Yes, 3 ≥ 3 for green |
| 2 | 3 | Yes, 3 ≥ 3 for red |
| 1 | 4 | Yes, 4 ≥ 3 for red |
| 0 | 5 | Yes, 5 ≥ 3 for red |
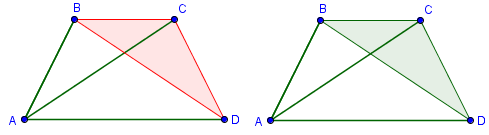
We take the case that exactly three are friends as shown in the second figure. It does not actually matter whether E and F are friends or strangers. In the proof, we only need vertices A, B, C and D.
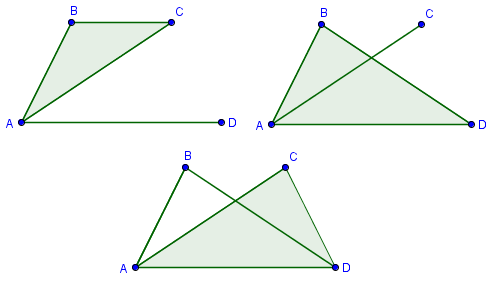
Now, B, C, and D can be connected by 3 edges that are either green or red. The possible color combinations are (1) 3 reds, (2) 3 greens, (3) 2 greens and 1 red, and (4) 1 green and 2 reds. In order to prove our claim, we need to show that in each case, at least one triangle is formed whose edges have the same color. The first two cases are obvious as shown below, 3 reds on the left, and three greens on the right. This means that the only cases left are 2 greens 1 red and 1 green, 2 reds.
Notice that having only 1 green edge connecting any of B, C, and D form a green triangle as shown in the figures below. This already proves the remaining two cases because both of them have green edges.
This proves that out of 6 persons either 3 are friends or 3 are strangers.