Fractions with Terminating and Non-Terminating Decimal Representations
Another representation of rational numbers aside from fractions is the decimal form. Every fraction has a decimal representation:
,
,
and
.
Notice that some of the fractions above are terminating, while the others are repeating decimals. The fractions and
have only one decimal place, while
and
have infinitely many (Can you see why?). Now, given a fraction, can we determine if it’s a terminating or non-terminating decimal without dividing?
Delving Deeper
First let us examine the characteristics of terminating decimals, say 0.125. The easiest way to convert this decimal into fraction is by dividing a whole number by a power of 10:
.
It is easy to see that all terminating decimals can be converted to a fraction of this form. Several examples are
,
,
.
From these representations, we are pretty confident that all terminating decimals can be expressed as
.
But notice that and
are also terminating decimals, so we can also conjecture that maybe, fractions with denominators of 2 and 5 are terminating decimals. Intuition tells us that they are indeed. An integer divided by 2 gives an integer or an integer plus a 0.5 and an integer divided by 5 gives an integer or an integer plus 0.2. Now, are fractions whose denominators are powers of 2 or powers of 5 terminating decimals? Note that we already know that fractions whose denominators are powers of 2 and powers of 5 are terminating if the powers are equal because
.
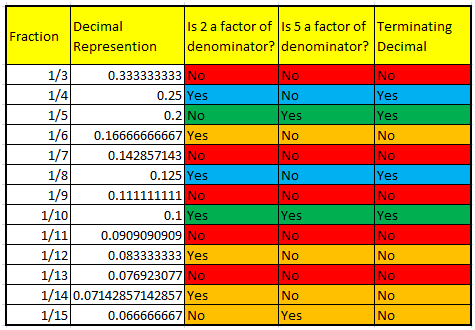
From the discussion above we have a bit of clue. We know that terminating decimals have something to do with fractions whose denominators have factors 2, 5, (or 10). To strengthen our hunch, we take all the unit fractions whose denominators are less than 16 and see what happens.
From the table above, we can observe the following:
- Fractions whose denominator does not include 5 and 2 as factors are non-terminating decimals.
- Fractions whose denominator is a power of 2 (¼, and 1/8) are terminating decimals.
- Even not on the table, we can also test fractions whose denominator is a power of 5 (1/5, 1/25, 1/125) and would easily see that they are terminating decimals.
- Fractions whose denominator includes 2 as a factor and includes a factor not equal to 5 are non-terminating decimals (e.g. 1/6 and 1/14).
- Fractions whose denominator includes 5 as a factor and includes a factor not equal to 2 (1/15) are non-terminating decimals.
From these observations, we can make the following conjecture:
A fraction is a terminating decimal if its factors are 2 or its powers, 5 or its powers, or both.
In the next post, we will have more discussions and we will refine our conjecture.