We say that a set is countably infinite if we can pair the elements with set of counting numbers 1, 2, 3, and so on. Believe it or not, the number of positive integers and the number of integers (both negative and positive including 0) have the same number of elements. It is because we can pair them in a one-to-one correspondence such as shown in the below.
As shown on the table, if we continue indefinitely, we know that we can pair each counting number with an integer in a one-to-one correspondence without missing any element.

Using this concept, we show intuitively that the number of points on two line segments is equal even if they have different lengths. We can do this by showing that for each point on segment 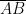 , there is a corresponding point on segment
, there is a corresponding point on segment 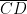 . » Read more
. » Read more
