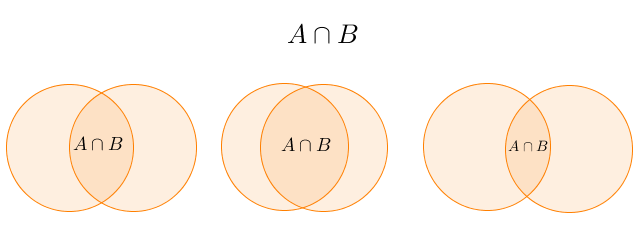Misconception About Venn Diagrams
Last year, I had a good discussion with some teachers about Venn diagrams. Several teachers commented that I should change the diagram below because it might give an impression that the number of rational numbers is the same as the number of irrational numbers. Sadly, I was not sure if I was able to explain my point. Anyway, below is an extended explanation to those comments.

Venn diagrams usually represent the logical relationships among sets. They do not concern with their cardinality (the number of elements). For example, if sets A and B have common elements, then their relationship can be represented by any of the three Venn diagrams below. In creating Venn diagrams, you do not represent if there is only one common element, or there are many: you are representing if there are common elements or there are none.
Further, even if we want to represent the relationship between the set of rational and irrational numbers with Venn diagrams considering their cardinality, it would be impossible to do so. This is because the number of irrational numbers from 0 to 1 is greater than the set of all rational numbers. It means that in two dimensions, the rational numbers is a dot in a plane of irrationals that extends infinitely on all directions.