Understanding Hilbert’s Grand Hotel Paradox
Long ago, in a land far away, there was a grand hotel where there were infinitely many rooms. This hotel was attended by a brilliant manager.
One night, a guest arrived, but the hotel was full — each room was occupied by one guest. The newly arrived guest asked if a spare room was available. “Of course we have, we are the Infinite Grand Hotel. There is always a room for everyone,” the manager said proudly.
Now since each room was occupied by a guest, the manager requested the guest in Room 1 to move to Room 2, the guest in Room 2 to move to Room 3, the guest in Room 3 to move to Room 4, and so on. Basically, he told every guest in Room n to move to Room n + 1. Since the hotel had infinitely many rooms, there was no problem in moving, there was always a room to move to. This left Room 1 vacant, and therefore, the guest was accommodated. The guest was happy. The manager was happy.
The next night, a bus of 60 passengers arrived and they asked for one room for each passenger. The same thing happened. The manager requested the guest in Room 1 to move to Room 61, the guest in Room 2 to move to Room 62, and every guest in Room n to move to Room n + 60. Since the hotel had infinitely many rooms, there was no problem in moving, there was always a room to move to. This left 60 rooms vacant and therefore the hotel accommodated the 60 new guests. Everybody was happy. The manager was happy.

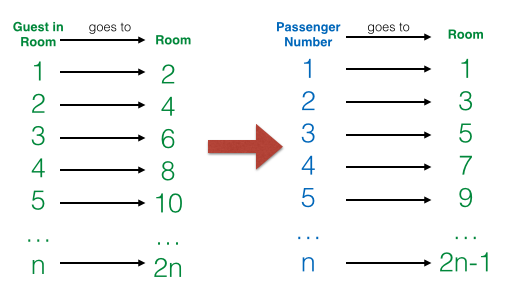
The next night, a bus infinitely long with an infinite number of passengers arrived. This looked like a big problem, but the manager shrugged it off. He requested the guest from Room 1 to move to Room 2, the guest from Room 2 to move to Room 4, the guest from Room 3 to move to Room 6 and all the guest in Room n to move to Room 2n. The guests didn’t mind moving. This left all the rooms with odd numbers vacant.
After everybody had moved, the manager assigned every passenger to the odd numbered rooms. He assigned Passenger 1 to Room 1, Passenger 2 to Room 3, Passenger 3 to Room 5, and Passenger n to Room 2n – 1. Since there are countably infinitely many odd numbers, and countably infinitely many rooms (see diagram above), the passengers can be assigned in one-to-one correspondence with the odd-numbered rooms. There was no problem of moving in, there’s always a room for everyone. Everybody had a room and everybody was happy. The manager was happy.
Infinite Buses, Each with Infinite Number of Passengers
The next night, an infinite number of buses arrived, each of which had an infinite number of passengers. This looked like a very big problem. The manager thought about it for a while.
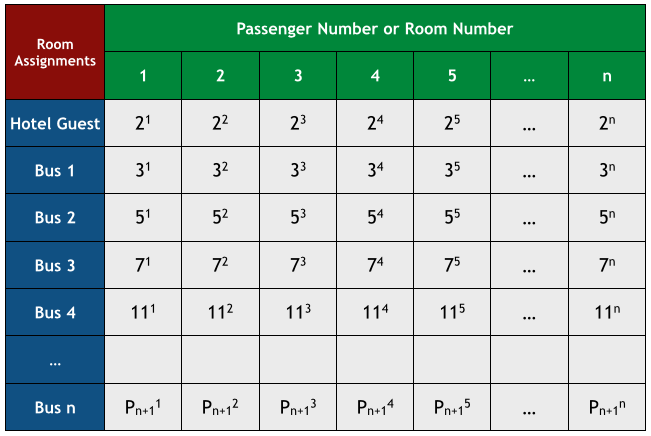
After a little bit of thought, the manager remembered from his math class that there are infinitely many primes. So, he thought that he could assign each bus to a prime number; he cleverly made the following room assignment scheme.
1.) He assigned all the guests in the hotel to the prime number 2. Then, he told the guest in Room 1 to move to Room or Room 2, the guest in Room 2 to move to Room
or Room 4, the guest in Room 3 to move Room
or Room 8, and every guest in Room
to move to Room
. So, the guest at Room 10 goes to Room
or Room 1024.

2.) Next, he assigned Bus 1 to the second prime number which is 3, Bus 2 to the 3rd prime number which is 5, Bus 3 to the 4th prime number, and Bus n to the th prime number . This means that Bus 100 will be assigned to 101st prime number which is 547. Since there are countably infinitely many prime numbers, all the buses can be assigned in one-to-one correspondence with the the prime numbers as shown in the previous diagram.
3.) Lastly, just like in 1, each guest in each bus was assigned to the room number which is a power of prime, the prime number in which the bus is assigned to. For example, what is the room number of Passenger 3 in Bus 4? Bus 4 is assigned to the 5th prime number which is 11. This means that the Passenger 3 goes to Room or Room
. What is the room number of the 12th passenger in the 1000th bus? Well, you have to look for the 1000th prime and then raise it to the 12th power. Notice from the table below the correspondence of the bus and the prime numbers, as well as the passenger numbers and the room numbers.
So, each bus had a corresponding prime number and each passenger number had a corresponding power of prime. This means that each passenger in all the buses had a room in the hotel. Everybody was happy.
The manager was NOT happy.
WHY?
After all the brilliant schemes that he had done, the manager realized that he had a gift in mathematics. He quit his job and became a mathematician (Just kidding).
Final Note
The hotel was occupied by guest from infinite number of buses, but surprisingly, there were still vacant rooms in the hotel. Notice that the room that were occupied were rooms that are power of primes. So, in the first 20 rooms, Rooms 6, 14, 15, and 18 were still vacant since they are not power of primes.
The problem above is called The Hilbert’s Grand Hotel Paradox. It was created by David Hilbert to illustrate the counterintuitive properties of infinite sets.
In the next post, I will discuss the mathematics involved in this brilliant problem. So, keep posted.
Image Credits: MathCS.org, Chinabuses.com