The Geometric Representation of Greatest Common Factor
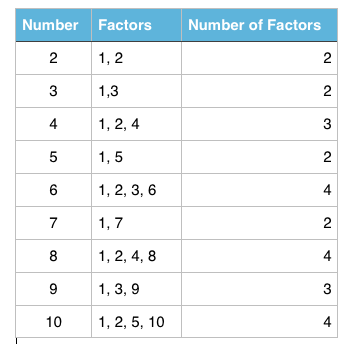
A factor is an integer that divides another integer. The number 6 is a factor of 12 since 6 divides 12. It is easy to see that 1, 2, 3, 4, and 12 are also factors of 12. Looking at the numbers in the tables below, we can see that some numbers have only 2 factors, 1 and itself. These numbers are called prime numbers.
Two or more numbers can have common factors. For example, let us consider the factors of 12 and 18.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 18: 1, 2, 3, 6, 9, 18
From the list above, we can see that the common factors of 12 and 18 are 1, 2, 3, and 6. The greatest among the factors is 6. As we have learned in elementary school mathematics, 6 is called the Greatest Common Factor (GCF) or Highest Common Factor (HCF) of 12 and 18.
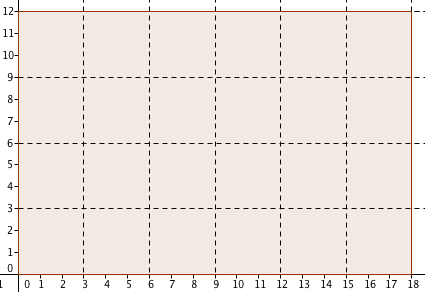
If we let 12 and 18 be the width and length of a rectangle, then how do we interpret the factors?
Notice that if we want to find the factors of two numbers, we are looking for a number that divides both. If we divide 18 by 1 and 12 by 1, then we can have lengths measuring 1 unit. So, the factor 1, represents the length of the squares that can be made to cover the rectangle without cutting.
Clearly, we can also use the other factors to create squares that will cover the 12 by 18 rectangle. For instance, in the next figure, we use squares with side length 3.
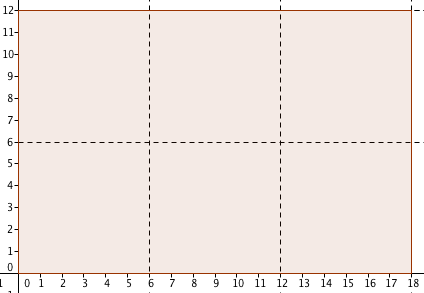
Finally, if we want to cover the rectangle with the largest squares without cutting, then we have to cover it with a 6 by 6 square where 6 is the GCF of the length and the width.
From the discussion above, we can conclude that the geometric representation of the factors of two numbers 
The geometric representation can be extended to three dimensions. Can you imagine the meaning of the factors and greatest common factor of 3 numbers in 3D?