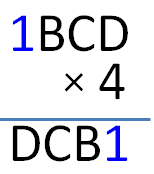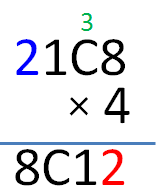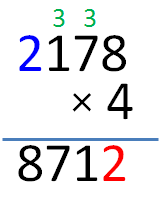Solving Problems by Eliminating Impossible Cases
One of the strategies in solving problems is to divide them into cases and see if you can eliminate some impossible cases. In this post, I will discuss a popular classic problem which I found the solution to be interesting.
Problem
If A, B, C, and D are distinct non-zero digits, find their values if ABCD × 4 = DBCA.
If you have not encountered this problem before, you might want to solve it first before reading the solution below.
Finding the Value of A
Solution
One of the most obvious hints of the problem is that the value of A is only limited to 1 and 2. Why? Because if A is greater than 2, 4 × A will become a 2-digit number. This will make the product of ABCD × 4 a 5-digit number which does not satisfy the problem.
If A = 1, then given becomes 1BCD × 4 = DCB1 .Now, this is impossible because the ones digit of 4 multiplied by D should be even. Therefore, A must be 2.
Finding the Value of D
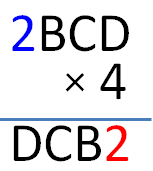
Now that we found the value of A, the next clue is finding the value of D since we already have 2 as the ones digit of the product.
Solution 1
It is likely that D = 8 since it is the product of 2. However, it is also possible that there is a carry over from 4 × B if its product is more than 10. If so, the only possible carry over is 1 since if it is greater than 1 it will make the product a 5-digit number.
Now, suppose 1 is the carry over, then D = 4 × 2 + 1 = 9. However, this is not possible since the product of D and 4 has 2 as its ones digit. Therefore, the only possible value for D is 8.
Solution 2
We look for the value of D such that the ones digit of the product of D is 2. We calculate all possible cases as shown below.
4(0) = 0
4(1) = 4
4(2) = 8
4(3) = 12
4(4) = 16
4(5) = 20
4(6) = 24
4(7) = 28
4(8) = 32
4(9) = 36
As we can see, there are two possible cases, D = 3, and D = 8. Clearly, D cannot equal 3 because it should be the product of 4 and 2 and a possible carry over which can only be equal to 1. Now, for it to be 3, the carry over must be 5, but the sum 8 + 5 = 13 which will make the product a 5-digit number.
Therefore, D = 8.
Finding the value of B
Solution 1
From above, D = 4 × 2 = 8, means that we did not carry over from the product of B. This means that the product of B and 4 is less than 10. So, the only possible values for B are 1 and 2. But A is already equal to 2 and from the given, A, B, C and D are distinct digits.
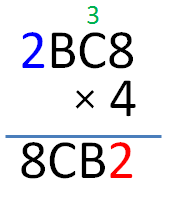
So, B = 1.
Solution 2
From above, D = 4 × 2 = 8, means that we did not carry over from the product of B. This means that the product of B and 4 is less than 10. So, the only possible values for B are 1 and 2
We find the values of B by getting the ones place of the result of 4C + 3.
4(0) + 3 = 3
4(1) + 3 = 7
4(2) + 3 = 11
4(3) + 3= 15
4(4) + 3= 19
4(5) + 3 = 23
4(6) + 3 = 27
4(7) + 3 = 31
4(8) + 3 = 34
4(9) + 3 = 35
The only value less than 3 is 1. So, B = 1.
Finding the value of C.
From the two cases above, 11 and 31, C = 2 or C = 7. Since A, B, C, and D are distinct digits and since and A = 2, it must be the case that C = 7.
Therefore, the correct answer from the problem above is 2178. So, 2178 × 4 = 8712.
The problem above shows how some problems can be shown by actually eliminating impossible cases.