Understanding the Monty Hall Problem
The Monty Hall Problem is one of the famous puzzles that is not very easy to understand. When Marilyn vos Savant (listed as Highest IQ by Guiness) posted this question in “Ask Marilyn” of Parade magazine, 10,000 readers including 1000 PhD holders wrote to the magazine asserting that Marilyn was wrong despite explanations and mathematical calculations shown. The Monty Hall problem is shown below.
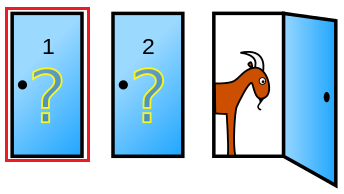
The Monty Hall Problem
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?
Note: The assumption in this problem is that once you have chosen, the host will always show you the door that contains a goat.
Most people will answer that switching doors doesn’t matter since there is a 50% chance that the car is in one of the doors. But that is not the case.
Explanation
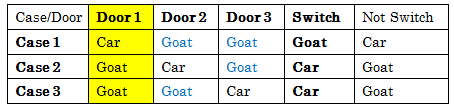
There are three possible cases: the car is either in door 1, 2, or 3 as shown in the table below. Now, suppose we chose Door 1, we have the following cases.
Case 1
- The host can either show you Door 2 or Door 3 since they are both goats.
- If you SWITCH, you get a GOAT .
Case 2
- The host shows you Door 3.
- If you switch, you get Door 2 which is a CAR (sure win).
Case 3
- The host shows you Door 2.
- If you switch, you go to Door 3 and you get a CAR.
As you can see, in choosing Door 1, if you don’t switch, you will only win in Case 1. If you switch, you win in Cases 2 and 3.
This is also similar when you choose Door 2. If you don’t switch, you will only win in Case 2, while you win in Cases 1 and 3 if you switch.
If you choose Door 3, you only win in Case 3 if you don’t switch, while you win in Cases 1 and 2 if you switch.
Therefore, in any case, the probability of winning when switch is twice that of when not switching.