Why the Area of a Rhombus is Half the Product of its Diagonals

March 4, 2015 GB High School Geometry, High School Mathematics

A rhombus is a parallelogram with four congruent sides. Since it is a parallelogram, it has also all the properties of a parallelogram. One of these properties is that the diagonals bisect each other. That is, they divide each other into two equal parts.

Another property of a rhombus is that the diagonals are perpendicular. So, summarizing all the properties above, if we have rhombus $ABCD$ , then,

$\overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DA}$ .

and

$\overline{AC} \perp \overline{BD}$ .

From the figure below, it is clear that if we divide the parallelogram into two triangles, $ABC$ and $ACD$ , $\overline{BE}$ and $\overline{DE}$ are their altitudes because they are perpendicular to $\overline{AC}$ .

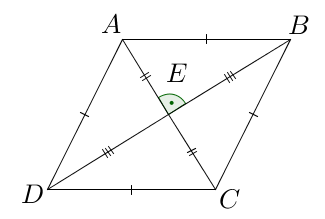
area of parallelogram

To find the area of parallelogram $ABCD$ , first we find the area of triangle $ABC$ , and then multiply it by 2. This is because triangle $ABC$ is congruent to triangle $CDA$ by SSS congruence (can you see why?).