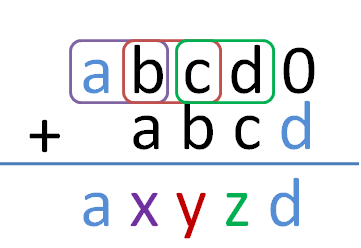Why the Multiplication by 11 Trick Works
One of the famous tricks that you have probably known is how to multiply numbers by 11. If we multiply a 2-digit number by 11, we copy the ones digit to the ones digit of the product, add the ones and the tens digit and place the sum in the tens digit of the product, and then copy the tens digit to the hundreds digit of the product. For example, if we multiply 34 × 11.
(1) We copy 4 and place it in the ones digit of the product.
(2) Add 3 and 4 = 7 and place it in the tens digit of the product.
(3) Copy 3 and place it in the hundreds digit of the product.
Therefore, 34 × 11 = 374.
In case the sum is more than 10, we carry over to the hundreds digit of the product. For example 87 × 11 gives a product of the following digits.
ones digit: 7
tens digit: 8 + 7 = 15
We carry 1 to the hundreds digit.
hundreds digit: 8 + 1 = 9
We can generalize this to numbers with larger number of digits. For example, in multiplying 251 by 11, we can copy the first and last digits and add the adjacent digits. Below are the digits of the product.
ones digit: 1
tens digit: 5 + 1 = 6
hundreds digit: 2 + 5 = 7
thousands digit: 2
So, the final answer is 2761.
Why does the method work?
We can see why the method works by examining the standard algorithm of multiplication. Multiplying numbers by 11 is the same as multiplying it by 10 and then adding to the number. If we have a number abcd where a, b, c, and d are digits, for example, and we multiply it by 11, the we can multiply it by 10 and then add abcd.
That is abcd × 10 = abcd0
And the placement of the numbers will look like the one below.
Notice that the ones digit d and the digit with the highest place value a are copied in the sum. Then the other digits are the sum of the adjacent digits. In the case above, the digits x = a + b, y = b + c, and z = c + d.
This shortcut algorithm will work for all positive numbers. This is because multiplying any number by 10 will move all the numbers one place value to the left as 0 is added on the right. Adding the original number will result to the alignment as shown above.