Understanding If-Then Statements
If I get my bonus, then I will buy a car.
If I become 30, then I will get married.
If , then
.
The statements above are examples of an if-then statement. An if-then statement is also called a conditional statement. A conditional statement is of the form if then
where
and
are statements and in which
follows from
. As shown above, conditional statements can be seen in real life or in mathematics.
In a conditional statement, the statement following if is called the antecedent (or hypothesis), while the statement following then is called the consequent (or conclusion).
Conditional statements have their truth values just like, and, or and not. To examine their truth values, let us consider the third conditional statement above. In this statement, we can assign as
and
as
.
First, notice that for all values of if
, then
. This makes the entire conditional statement true. For example, if
, then
. This makes
true,
true, and the whole conditional statement true.
Second, we can also see that for all value of , if
, then
. This conditional statement is true. For example, if
, then
. This makes
false,
true, and the whole conditional statement true.
Third, we know that if , then
. This makes both
and
false and the whole conditional statement true. Notice that the only case that we have not tested yet is the statement where p is true and q is false. Now, consider the following statement: If
, then
.
If we can find one counterexample to this statement, then the entire conditional is false. Can you find a counterexample?
If we let ,
, and
is false. Since this is a counterexample, this means that the conditional is false.
Summarizing the truth values above, we can have the following table.
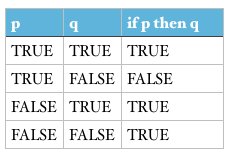
From here we can define the if then statement.
An if-then statement is a statement that is false when the antecedent is true and the consequent is false, and true in all other cases.
Reference: Precalculus and Discrete Mathematics (1992), UCSMP