How to Represent Inequalities in One Variable
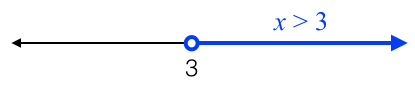
The inequality x > 3 means all numbers greater than 3. The set of numbers that makes the inequality true is called the solution set of the inequality. An instance of this numbers such as 4 is a solution to x > 3.
The graph of x > 3 is shown on the number line below. The “empty circle” means that the solution does not include 3. The highlighted part of the number line (blue ray) means that it includes all real numbers greater than 3 and the arrow indicates that it goes up to infinity.
Another notation to represent x > 3 is (3, ∞). The number on the left side is the lower bound and the right side is the upper bound. This notation means from 3 up to infinity. In addition, the symbol ( denotes that 3 is not included in the solution. Therefore, the interval (5,7) means all real numbers from 5 to 7, not including 5 and 7. The infinity symbol always takes the ( and ) symbols.
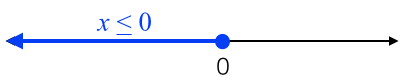
When we say x ≤ 0, this means all numbers less than 0, including 0 itself. On the number line, the inclusion of 0 is represented by a “colored circle” as shown in the second figure. Since this includes all numbers from negative infinity up to 0, it can be represented in the interval notation by (-∞, 0]. The ] symbol means near 0 means that 0 is included.
Using these notations, we can show the graph of -3 < x <=1 below. This means that x is between – 3 and 1, does not include 3, and includes 1. In interval notation, this can be represented as (-3,-1].
The additional operator or maybe included for solutions of numbers just like the one shown on the graph below. This can be represented by two inequalities x < -2, x ≥ 4.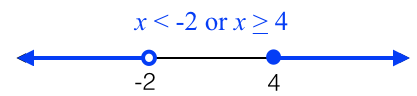
Notice that we cannot use the and operator in this kind of inequality since placing an “and” will mean that the solution will make both the inequality by true. Of course a number cannot be less than -2 and at the same time greater than 4. So, or is the correct operator making the inequality
x < -2 or x ≥ 4.
In interval notation, this can be written as (-∞, -2) ∪ [4, ∞) where ∪ is the union symbol for sets.