How to Add Integers Using the Number Line
There are several ways that we can visualize addition of integers. One way is to use the number line. If you can see the pattern in this method, it is easier to see the sign of the sum of two integers. To be able to use this method to add integers, first we should think of integers as movements on the number line. We can think of the positive integers as movement to the right and the negative integers as movement to the left.
In adding integers, the representation of the first movement should start from 0. The next movement should start from where the previous movement stopped.
Some Examples
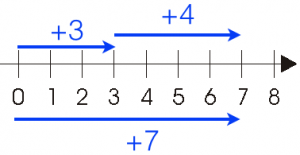
Example 1:
First, from 0, we move 3 units to the right and from where it stopped, we move another 4 units to the right.
The last movement stopped at . This is the same as moving 7 units to the right of 0 which means that
.
So, what is the rule in adding two positive integers?
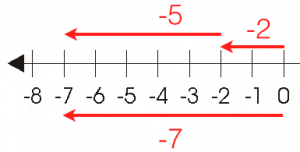
Example 2:
From 0, we move 2 units to the left and from where it stopped, we move another 5 units to the left.
The movement stopped at . This is the same as moving 7 units to the left. This means that
.
So, what is the rule in adding two negative integers?
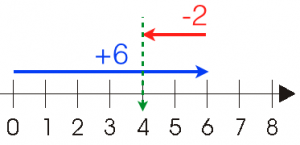
Example 3:
From 0, we move 6 units to the right, and from where it stopped, we move 2 units to the left.
We stopped at ; therefore,
.
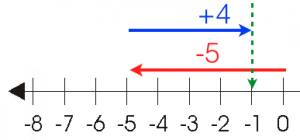
Example 4:
From 0, we move 4 units to the left and from where it stopped, we move 2 units the the right.
We stopped at . Therefore,
.
Using this method, it is easy to visualize if the sum of an addition problem is positive or negative. For example, in the addition , we move 8 units to the left of 0 and then 5 units to the right. After these movements, it is clear that we are still to the left of 0 since the distance of the movement to the left is greater than the distance of the movement to the right. Recall that this distance; that is, the distance from 0 to a number on the number line is also the absolute value of the number. So, the sign of the sum of a positive integer and a negative integer is the same as the sign of the integer with a larger absolute value.
In adding integers with more than two addends, it is sometimes easier to add the integers with the same sign first, then perform the final addition using two addends. For example, if we have , we add first
, then add
. Finally, we add
.