Derivation of the Area of a Rhombus

A rhombus is a parallelogram whose sides are congruent. The diagonals of rhombus are perpendicular to each other. They also bisect each other. In this post, we are going to find the general formula for finding the area of a rhombus using these properties. We are going to learn two methods.

Method 1

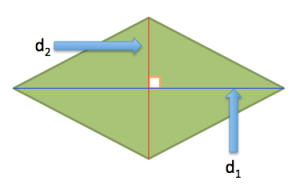
Consider the rhombus below.

We can divide it into two congruent triangles using diagonal . Since the diagonals of a rhombus are perpendicular to each other, we can use as base and one half of as the height of the upper triangle (Why?). If we let be the area of the upper triangle, then, calculating its area, we have 

.

Now, we only calculated for the area of the upper triangle. Since the area of the rhombus is twice the area of the upper triangle, we multiply by 2. That is,

.

Method 2

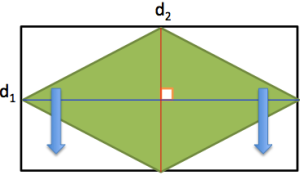
The second method is to enclose the rhombus with a rectangle. This can be done by drawing lines parallel to the diagonals and passing through the vertices (see figure below).

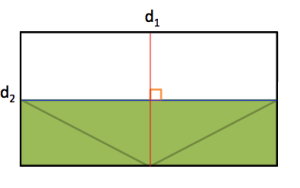
The two diagonals divide the rhombus into four triangles. Notice that if we move the two triangles as indicated by the arrow in the figure above, then we have transformed the parallelogram into a rectangle.

Now, the length of the rectangle is and the width is . The area of a rectangle is equal to the product of its length and its width, so

.

From the two methods above, we have shown that the area of a rhombus is equal to half the product of the length of the its two diagonals.