The Algebra and Geometry of Square Root

March 5, 2016 GB High School Algebra, High School Mathematics

If we have a square with a given area, then we can find the length of its side. For example, a square with area 4 square units has a side length of 2 units. In other words, in finding the side length of a square with area 4 square units,we are looking for a number that is equal to 4 when squared.The number that when squared is equal to 4 is called the square root of 4 and is written as $\sqrt{4}$ . From the discussion above, we now know that

$\sqrt{4} = 2$ .

It is easy to see that $\sqrt{1} = 1$ , since $1^2 = 1$ and $\sqrt{0} = 0$ since $0^2 = 0$ .

The square root of the two numbers above are integers, but this is not always the case. For instance, $\sqrt{2}$ is clearly not an integer since $1^2 = 1$ and $2^2 = 4$ . This means that $\sqrt{2}$ is somewhere between 1 and 4. What about $\sqrt{5}$ ?

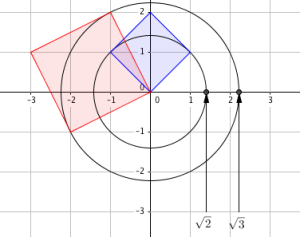
If we want to find the lengths $\sqrt{2}$ and $\sqrt{5}$ , we can go back to the square problem above. This time, we want to draw two squares whose areas are 2 square units and 5 square units. It will not take long to see that the sides of the squares are not along the grid as shown in Figure 1. Notice that the smaller square has area 2 square units (4 half squares) and the larger square has area 5 square units (1 square and 4 right triangles from 1 by 2 rectangles). It follows that the lengths of the sides of these squares are $\sqrt{2}$ and $\sqrt{5}$ units.

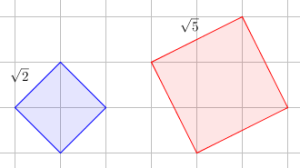
Figure 1 – Squares with area 2 square units and 5 square units

We can measure the lengths of sides of the squares using a ruler, but we can also place one of the vertices of each square on the origin and use a compass to locate their positions on the number line as shown in Figure 2. As we can see, the lengths of the radii of the two circles are equal to the lengths of the sides of the squares, so we can determine their locations on the number line. Further, we can use a calculator to know approximate numerical values of these lengths: $\sqrt{2} \approx 1.414$ and $\sqrt{5} \approx 2.236$ *.

Figure 2 – Location of square root of 2 and square root of 5 on the number line.

We can relate the discussion above to the equation $y = x^2$ since getting the value of $x$ requires calculating the square roots of both sides. Notice that for $y = 9$ , there are two x’s: $x = 3$ and $x = -3$ . If we graph $y = x^2$ , we get a parabola. Let the y coordinate of the graph be $a$ , then there are two possible x coordinates, which are $\sqrt{a}$ and $- \sqrt{a}$ . On the contrary, it should be noted that the square of a number is always positive, so we cannot get the square root of a negative number**.

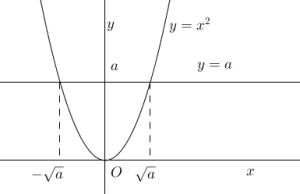
Figure 3 – The graph shows that a positive number has two square roots, one positive and one negative.

The larger the square, the longer its side, so it also follows that for positive numbers a and b, if $a^2 > b^2$ , then $a > b$ . In addition, the longer the side of a square, the larger it is, so we can also say that if $a > b$ , then $a^2 > b^2$ .

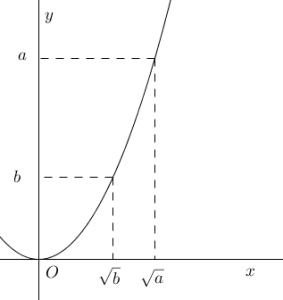
Figure 4 – The graph shows that if the square root of a is greater than the square root of b, then a is greater than b.

The preceding relationship is illustrated in the graph of $y = x^2$ in Figure 4. If $\sqrt{a}$ is at the right of $\sqrt{b}$ on the x axis (that is $\sqrt {a} > \sqrt {b}$ ), the $a$ is above $b$ on the y-axis which means $a > b$ .

* The symbol $\approx$ means approximately equal to.
** Negative numbers have square roots, but they are not real numbers. We call them imaginary numbers.

Leave a comment area of a square, side length of a square, square of a number, square root of a number

The Algebra and Geometry of Square Root

Leave a Reply Cancel reply