How to Change Number Bases Part 2
In the previous post, we have learned how to change numbers form one base to other. In this post, we are going to discuss more examples of number bases particularly the two number systems used in computers: the binary and the hexadecimal system.
The Binary Number System
The binary number system has base 2 and only uses 1 and 0 as digits. The binary number 1101 in expanded form is
or
8 + 4 + 0 + 1 = 13 in base 10. If we want to convert base 10 numbers to base 2, then we look for the highest multiple of the powers of 2 and subtract from the number each time until the difference is 0.
Example: Convert 74 to base 2.
The highest number that can be subtracted from 74 is . So, just like in the previous post, we can create a table with the largest number as
as shown below. Since, we can subtract
from 74, we write 1 under
.
Subtracting, we have . We cannot subtract
and
from 10, so we write 0 under these numbers.
We know that , so we write 1 under them and write 0 in the remaining cells. The final answer is shown in the next table.
From the table, this means that .
Exercises:
1.) Convert 213 to binary.
2.) Convert 100110 to decimal
The Hexadecimal Number System
The hexadecimal number system or the base 16 number system uses 0, 1, 2, all the way up to 15 as digits.
In base 10, when we talk about digit, we are taking about one number. One thing that probably comes to your mind is how do we deal with digits containing two digits in base 16? For example, in the hexadecimal number, is 14 a 1-digit number or a 2-digit number? To solve this problem, letters were used to denote digits from 10 to 15: A = 10, B = 11, C = 12, D = 13, E = 14 and F = 15. That means that the expanded form of E20A is
or 57344 + 512 + 0 + 10 = 58866 in base 10.
Just like in the previous examples, in converting base 10 numbers to base 16 numbers, we need to look for the highest multiples of powers of 16 and subtract each time until the difference is 0.
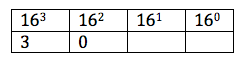
Example: Convert to base 16.
We know that , so we can only subtract multiples of
from 12452. Obviously, 12452 divided by 4096 will give an integral quotient of 3, so we write 3 under
in the table below.
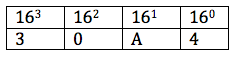
Now, . Clearly, we cannot subtract
from 164, so we put 0 under it.
Next, there are ten in 164, so we write A under it. Next, 164 – 10(16) = 4. So, we write 4 under
.
Exercise:
Convert 18B2 to base 10.
Convert 15000 to base 16.