Guest Post: Calculating Trignometric Values

High School Mathematics

Many students who start to learn Trigonometry often ask themselves how do we come to know that

\sin 30^\circ = \frac{1}{2} or \cos 45 ^\circ = \frac{\sqrt{2}}{2}

or for that matter any other trigonometric value?

Most of us would say use a trigonometric table or use a scientific calculator and you get the value. That’s okay, but the question still remains unanswered. How does a calculator come to know that \tan 15^\circ = 0.26794919... or how did the mathematicians create the entire trig tables when calculators were not invented? There should be some formula that tells us as to how the values are calculated. More importantly, can I, using a standard calculator, find the approximate value of let’s say \sin 50.5^\circ? Yes, there is a simple formula to find the value of sine of any acute angle. Though the formula does not give accurate results, it comes handy to know the value of \sin \theta  where 0^\circ \leq \theta \leq 90^\circ.

 \sin x ^\circ = \frac{4x(180 - x)}{40500 - x(180 - x)}.

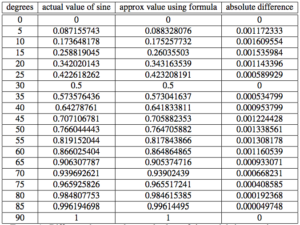
This rational approximate formula was discovered by Bhaskara I of India in the seventh century. This simple formula enables us to calculate the sine of any given acute angle (any even obtuse angle) with a maximum absolute error of 0.00163. 

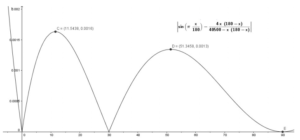
Trignometric Values

FIGURE 0.1. Difference between the actual sine value and the approximate value using the above formula

Here is the table showing the actual values of the sine function and their approximates:

screen-shot-2016-10-27-at-8-57-43-pm

TABLE 1. Difference between the actual values of sine and their approximates

Now using Bhaskara’s formula, we can derive the formula of cosine and tangent as follows:

cos x = \frac{4(90+x)(90 - x)}{ 40500 - (90+x)(90 - x)}

\tan x = \frac{x(180 - x)(x^2 +32400)}{(90+x)(90 - x)(x^2 -180x+40500)}

To find the sine values of obtuse angles use the identity \sin x = \sin(180 - x). So, if you have a standard calculator or if you are good in doing mental math, you can get fairly accurate values using Bhaskara’s formula. But if you require more accurate results, then use the Taylor / Maclaurin series. First convert the angle from degrees to radians using the formula x^c = \frac{\pi \times x ^\circ}{180}

\sin x = \sum^{\infty}_{n=0} \dfrac {(-1)^n} {(2n+1)!}x^{2n+1} = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} -\dfrac{x^7}{7!} + \dfrac{x^9}{9!} - \dfrac{x^{11}}{11!} + \cdots.

Of course, we can’t go on forever and we need to stop the above formula somewhere. More terms mean more accuracy. So suppose you want to find \sin 38^\circ , first convert 38^\circ into radians.

x^\circ = \frac{\pi \times 38}{180} = 0.6632.

The ! mark in the above formula is the factorial function. So, 3! = 3 \times 2 \times 1 = 6

\sin 38 ^\circ = \sin 0.6632 \approx 0.6632 - \frac{0.6632^3}{6} + \frac{0.6632^5}{120} - \frac{0.6632^7}{5040} + \frac{0.6632^9}{362880} - \frac{0.6632^{11}}{39916800}

\sin 38^\circ = 0.61564.

The actual value of \sin 38^\circ = 0.61566. The absolute difference being 0.00002. It should be noted that here the value of \pi and angle in radians are rounded to 4 decimal places. Again, more digits mean more accurate.

About the Author

My name is Sohael Babwani from Mumbai, India. I give private tuitions to schoolchildren. I teach all subjects including Maths. In the year 2004, I had written an article “An Extended Approach to the Julian and the Gregorian Calendar” This article was published in The Mathematical Gazette, London. I have made a blog/website http://www.babwani-congruence.blogspot.in/ explaining the same.

Leave a comment , , ,

Leave a Reply