Solving Rational Inequalities and the Sign Analysis Test
In this post, we are going to learn the steps in solving rational inequalities and see why we are doing them. For discussion’s purposes, let’s take the inequality
as an example. In solving rational inequalities, first we get its critical values, then use the values to determine the intervals, and finally, test the values in each interval to see if they satisfy the inequality or not. Those that satisfy the inequality are included in its solution set.
Getting the Critical Values
To get the critical values, we equate the numerator and the denominator of the inequality to 0 (if applicable). If we think of the inequality as a function, that is, if we let
,
then equating the numerator to 0 means getting the zeroes of that function. Graphically, the zeroes are the intersections of the graph of the function and the x-axis. In the example above, when we equate , we get
. This is where the graph will intersect the x-axis.
In equating the denominator to 0, we determine the values of where there are holes or vertical asymptotes. If we factor both the numerator and denominator completely, the zeroes of the factors that we can cancel are the holes, otherwise vertical asymptotes. In the given above, equating the denominator to 0 only gives us asymptotes.
,
.
From the equation above, the vertical asymptotes of the function are at and
. Now that we found all the three critical points, we plot them on the number line. These points divide the number line into four intervals.
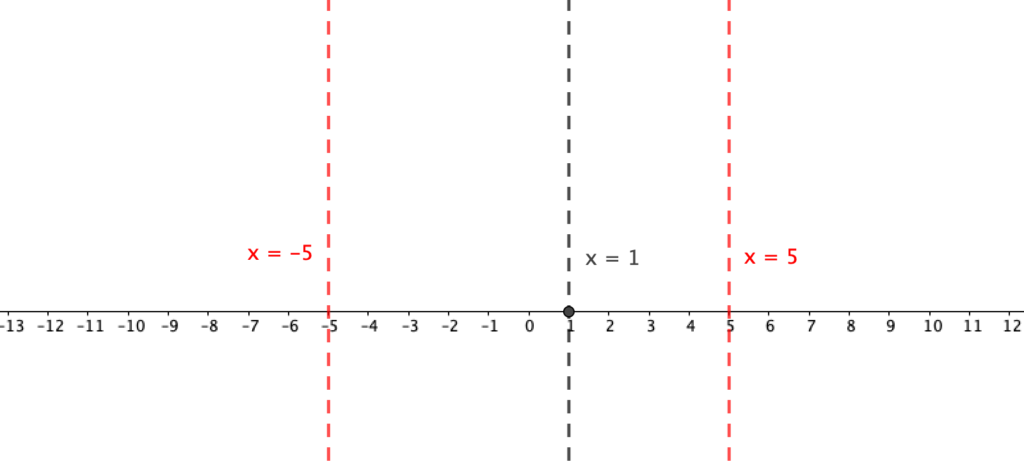
Sign Analysis Test
Now that we identified the critical values, we do the sign analysis test. In this test, we choose a number from each interval and substitute it to the inequality to see if the resulting value satisfies the inequality. Since , we are looking for values of
that will make the expression
either positive or 0.
In testing the intervals, if we choose ,
,
, and
. Substituting these values to the inequality give us
,
,
,
,
respectively. This means that the intervals containing and
are the solutions to the inequality.
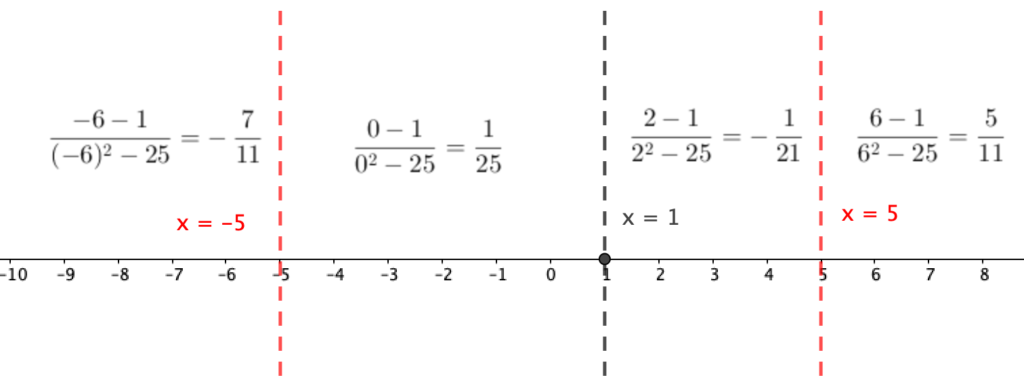
We now test the critical values and see if they are included in the solution set. In the inequality above, since will make the inequality 0, it is therefore included in the solution. However,
and
are not included as solutions because they will make the denominator 0 and will make the rational expression undefined. Therefore, the solutions are the intervals that contain positive values, includes
, and exclude
and
. In interval notation, the solution set is
.
Interpreting the Solution
We are looking for positive values of that will make the inequality
,
true and obtained the solution . In the function
,
the values which are greater than 0 are the parts of the graph above the x-axis. As we can see, these are the intervals and
.
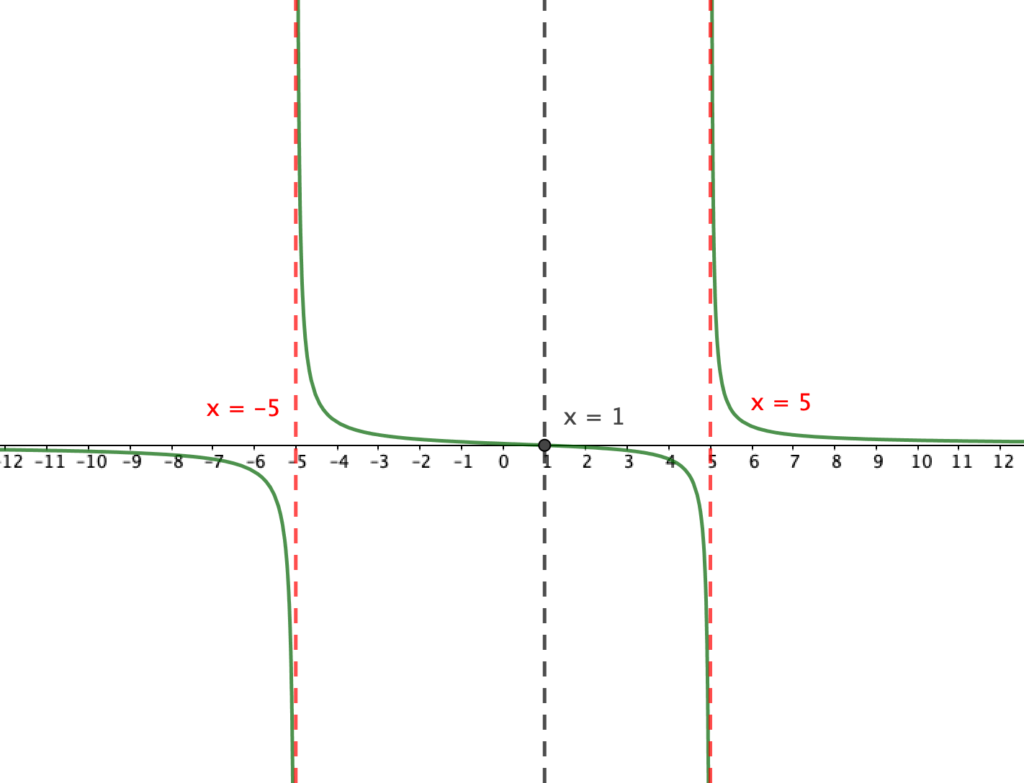
We can also verify the critical values and
from graph. They are vertical asymptotes. Lastly, the value
is the intersection of the graph and the x-axis.
