Understanding Sample Space and Sample Points
In tossing a fair coin, there are only two possible outcomes, a Head (H) and a Tail (T). If we let S be the set of all possible outcomes of this event, then, we write the set of possible outcomes as S = {H,T}.
If two fair coins are tossed, then the outcomes can be both heads {H,H} or both tails {T,T}. It can also be a head first then a tail {H,T}, or a tail first and then a head {T,H}. So, in tossing two coins, we have the set of possible outcomes S = {{T,T}, {T,H}, {H,T}, {H,H}}.
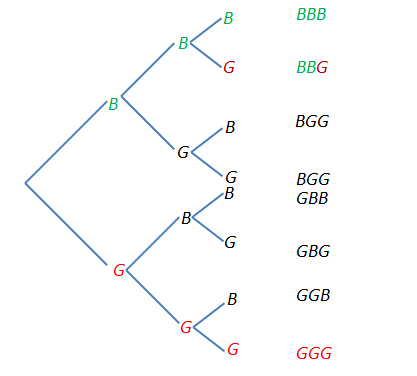
As the number of tosses increases, listing gets more difficult. One of the strategies that can be used to remedy this problem is by creating a tree diagram. The following problem is solved using a tree diagram. Notice that it is a three-coin tossing problem in disguise (try replacing B with H and G with T). » Read more