Tag: simplify negative exponents

11 Proven Proof Techniques Non-Math Majors Should Know

Fun and Jokes, Math Lite, Math Palette

Proofs is the heart of mathematics.  It is what differentiates mathematics from other sciences.  In mathematical proofs, we can show that a statement is true for all possible cases without showing all the cases. We can be certain that the sum of two even numbers is  even without adding all the possible pairs.

 

 funny math proof

For those who are “non-math people,” the proof techniques below will help you, but the “math people” are probably those who are going to enjoy them more.  » Read more

Leave a comment , , , , ,

Why is any number raised to 0 equals 1?

High School Algebra, High School Mathematics, Number Theory, Questions and Quandaries

Why is any number raised to 0 equals 1?

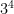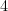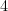If we raise a number to an exponent, we are multiplying it by itself a certain number of times.  For example, 3^4 means you have to multiply 3 by itself 4 times.   In exponential notation, we call 3 the base and 4 the exponent.

Shown below are examples of exponential expressions and their expansion.

2^3 = 2 \cdot 2 \cdot 2

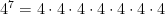
4^7 = 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4\cdot 4\cdot4

x^4 = x \cdot x \cdot x \cdot x

(a + b)^3 = (a+ b)(a+b)(a+b)

x^m = x \cdot x \cdot x \cdot \ldots \cdot x \cdot x (Multiply x by itself, m times)

The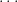\ldots symbol means “and so on.” It represents x’s that are missing.  It is convenient to use the said symbol for large values of m.

Multiplying Expressions with Exponents

If we want to multiply expressions with the same base, let us see what happens. For example, what will happen if we multiply 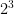2^3 and 2^5?

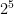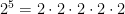From above, 2^3 = 2 \cdot 2 \cdot 2 and 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2. Multiplying the two expressions, we have

2^3 \cdot 2^5 = (2 \cdot 2 \cdot 2)(2 \cdot 2 \cdot 2 \cdot 2 \cdot 2) = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 2^8

From our computation, we can conclude that if we multiply to expressions with the same base, we have just have to add their exponents (Can you see why?). That is, for expressions 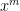x^m and x^n,

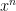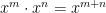x^m \cdot x^n = x^{m+n} (*)

Q1: What if the base of the two expressions are not the same? Will our formula above still apply?

Dividing Expressions with Exponents

What about dividing expressions with exponents? Suppose, we want to divide 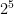2^5  by 2^3.

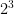We know that 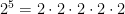2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 and 2^3 = 2 \cdot 2 \cdot 2. Dividing the two expressions, we have

\displaystyle \frac{2^5}{2^3}= \displaystyle\frac{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2}{2 \cdot 2 \cdot 2} = 2^2

Since, three 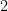2‘s are canceled out, we can therefore conclude that in dividing two expressions with the same base, we just have to subtract their exponents. That is, for expressions 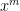x^m and x^n,

\displaystyle\frac{x^m}{x^n} = x^{m-n}. (**)

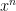What happens if the exponent of the denominator is larger? For example, \displaystyle \frac{2^2}{2^7}?

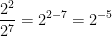From (**), \displaystyle\frac{2^2}{2^7} = 2^{2-7} = 2^{-5}.

Now, let us compare this result when we expand our expression:

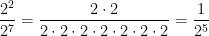
\displaystyle \frac{2^2}{2^7}= \displaystyle\frac{2 \cdot 2}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2} = \frac{1}{2^5}

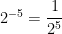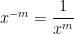Our observation tells us that, 2^{-5} = \displaystyle\frac{1}{2^5}. Therefore, x^{-m}= \displaystyle\frac{1}{x^m}.

Q2: In general, what is the value of \frac{x^m}{x^n} if m < n?

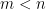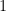What if the exponents of the numerator are equal? For instance, \frac{2^5}{2^5}. This is practically dividing the same number, so obviously the answer is 1. However, we can also use our conclusion above.

From (**), \displaystyle\frac{2^5}{2^5} = 2^{5-5} = 2^0 = 1

Conclusion

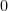Here we observe that raisingx (or any expression) to 0  means that the number of factors in the numerator and the number of factors in the denominator is the same. Therefore, 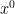x^0 can be expressed as x^{m-m} for any value of m. But from (**), x^{m-m} is equivalent to \displaystyle\frac{x^m}{x^m} = 1

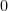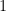Therefore, any number raised to 0 (with the exception of 0) equals 1.

Leave a comment , , , ,