The Algebraic and Geometric Proofs of Pythagorean Theorem

The Pythagorean Theorem states that if a right triangle has side lengths $a, b$ and $c$ , where $c$ is the hypotenuse, then the sum of the squares of the two shorter lengths is equal to the square of the length of its hypotenuse.

Figure 1 – A right triangle with side lengths a, b and c.

Putting it in equation form, we have:

$a^2 + b^2 = c^2$ .

For example, if a right triangle has side lengths $5$ and $12$ , then the length of its hypotenuse is $13$ , since $c^2 = 5^2 + 12^2 \Rightarrow c = 13$ .

Exercise 1: What is the hypotenuse of the triangle with sides $1$ and $\sqrt{3}$ ?

The converse of the theorem is also true. If the side lengths of the triangle satisfy the equation $a^2 + b^2 = c^2$ , then the triangle is right. For instance, a triangle with side lengths $(3, 4, 5)$ satisfies the equation $3^2 + 4^2 = 5^2$ , therefore, the said triangle is right.

Geometrically, the Pythagorean theorem states that in a right triangle with sides $a, b$ and $c$ where $c$ is the hypotenuse, three squares are constructed containing the sides of the triangle as shown in Figure 2, the area of the two smaller squares when added equals the area of the largest square (click here to see animation).

Figure 2 – The geometric interpretation of the Pythagorean theorem states that the area of the green square plus the area of the red square is equal to the area of the blue square.

One specific case is shown in Figure 3: the areas of the two smaller squares are $9$ and $16$ square units, and the area of the largest square is $25$ square units.

Exercise 2: Verify that the area of the largest square in Figure 3 is 25 square units.

Figure 3 – A right triangle with side lengths 3, 4 and 5.

Similarly, triangles with side lengths $(7, 24, 25)$ and $(8, 15, 17)$ are right triangles. If the side lengths of a right triangle are all integers, we call them Pythagorean triple. Hence, $(7, 24, 25)$ and $(8, 15, 17)$ are Pythagorean triples.

Exercise 3: Give other examples of Pythagorean triples.

Exercise 4: Prove that there are infinitely many Pythagorean triples.

Proofs of the Pythagorean Theorem

There are more than 300 proofs of the Pythagorean theorem. More than 70 proofs shown in Cut-The-Knot website. Shown below are two of the proofs. Note that in proving the Pythagorean theorem, we want to show that for any right triangle with hypotenuse $c$ , and sides $a$ , and $b$ , the following relationship holds: $a^2 + b^2 = c^2$ .

Geometric Proof

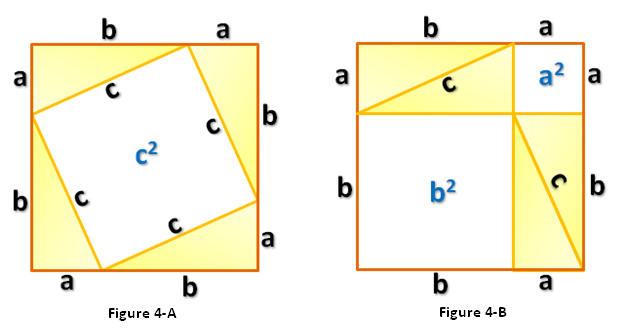
First, we draw a triangle with side lengths $a, b$ and $c$ as shown in Figure 1. Next, create 4 triangles identical to it and using the triangles form a square with side lengths $a + b$ as shown in Figure 4-A. Notice that the area of the white square in Figure 4-A is $c^2$ .

Figure 4 – The Geometric proof of the Pythagorean theorem.

Rearranging the triangles, we can also form another square with the same side length as shown in Figure 4-B.This means that the area of the white square in the Figure 4-A is equal to the sum of the areas of the white squares in Figure 4-B (Why?). That is, $c^2 = a^2 + b^2$ which is exactly what we want to show. *And since we can always form a (big) square using four right triangles with any dimension (in higher mathematics, we say that we can choose arbitrary $a$ and $b$ as side lengths of a right triangle), this implies that the equation $a^2 + b^2 = c^2$ stated above is always true.

Exercise 5: Prove that the quadrilateral with side length C in Figure 4-A is a square.

Algebraic Proof

In the second proof, we will now look at the yellow triangles instead of the squares. Consider Figure 4-A. We can compute the area of a square with side lengths $a + b$ using two methods: (1) we can square the side lengths and (2) we can add the area of the 4 congruent triangles and then add them to the area of the white square which is $c^2$ . If we let $A$ be the area of the square with side $b + a$ , then calculating we have

Method 1: $A = (b + a)^2 = b^2 + 2ab +a^2$

Method 2: $A = 4(1/2ab) + c^2 = 2ab + c^2$

Methods 1 and 2 calculated the area of the same square, therefore they must be equal. This means that we can equate both expressions. Equating we have,

$b^2 + 2ab + a^2 = 2ab + c^2 \Rightarrow a^2 + b^2 = c^2$