Have you ever wondered why manholes are circular?
The answer is simple. Using other shapes, it is possible for manhole covers to fall through the hole. For example, a square cover with side length 1 meter can fall through a square manhole even if the lip (stopper) makes the side length of the manhole less than that of its cover.
To explain further, suppose a 5-cm lip is placed on each side of the hole, then that leaves a square hole with side length 90 cm. Using the Pythagorean theorem, that hole has diagonal of more than 1.27 meters, large enough to swallow the cover (see 3rd illustration in the 1st figure) with a burp.
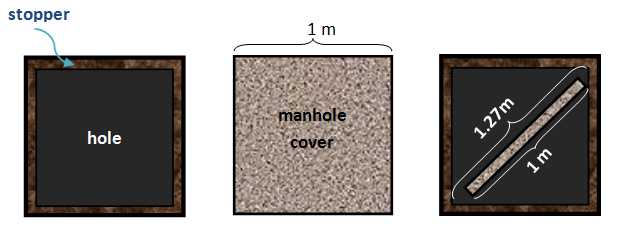
On the other hand, the constant diameter of a circular cover ensures that it does not fall through the circular hole no matter how roughshod (I hope I used the word correctly) it is moved by vehicles. » Read more
,
, and hypotenuse
, the following equation holds
.

