The Mathematical Reason Why Manholes are Round

Have you ever wondered why manholes are circular?

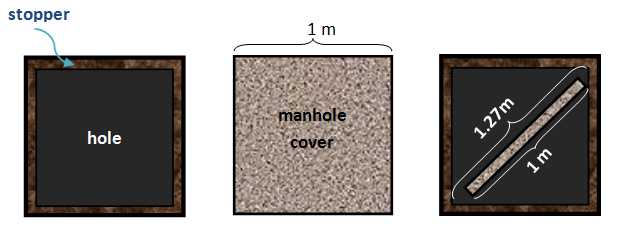
The answer is simple. Using other shapes, it is possible for manhole covers to fall through the hole. For example, a square cover with side length 1 meter can fall through a square manhole even if the lip (stopper) makes the side length of the manhole  less than that of its cover.

To explain further, suppose a 5-cm lip is placed on each side of the hole, then that leaves a square hole with side length 90 cm.  Using the Pythagorean theorem, that hole has diagonal of more than 1.27 meters, large enough to swallow the cover (see 3rd illustration in the 1st figure) with a burp.

On the other hand, the constant diameter of a circular cover ensures that it  does not fall through the circular hole no matter how roughshod (I hope I used the word correctly) it is moved by vehicles. 

In addition to the mathematical reason, manhole covers are heavy to lift, but if they are circular, they can be rolled easily from one place to another.

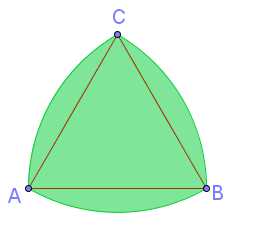
Aside from circles, there are special shapes that can also be used to cover manholes. One of the most popular shapes is the Reuleaux triangle shown above.  A Reuleaux triangle is a curve made from drawing arcs using the three vertices of an equilateral triangle as centers. That is, given an equilateral triangle ABC, use A as center and then draw arc BC. Repeat this process, using B as center and then using C as center to create a “triangular-shaped” curve.

Since the maximum length from one part of the curve to another is equal to the side length of the equilateral triangle, creating a stopper less than that length would ensure that the cover will not fall through a hole of the same shape.

***

Reference: http://www.coolquiz.com/trivia/explain/docs/manholes.asp