GeoGebra Tutorial 19 – Basic Spreadsheet Recording
This is the 19th tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, you might want to read first the GeoGebra Essentials Series.
A spreadsheet is a program that can be used to organize data in tables and perform mathematical computations. Recently, GeoGebra integrated spreadsheet in its graphical user interface. In this tutorial, we learn how to use the GeoGebra spreadsheet.
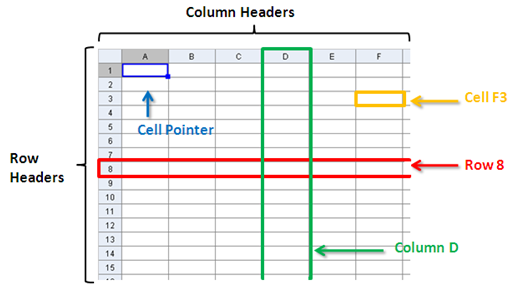
Figure 1
The figure above shows the different parts of a spreadsheet. The following are the descriptions. You should familiarize yourself with these terms because we are going to use them in this tutorial and the two more tutorials to come.
- Column – the horizontal division of the spreadsheet. Columns are labeled with letters.
- Row – the vertical division of a spreadsheet. Rows are labeled with numbers.
- Column/Row Headers – The part of the spreadsheet where the column/row labels are placed.
- Cells – the smallest unit in a spreadsheet, or the intersection of a column and a row.
- Cell Addresses – the name used to refer to a particular cell; that is, their column header and row header. For example, cell A1 is the cell on the first column and the first row. F3 is the cell with the orange box in Figure 1.
- Cell Pointer – a rectangular box that indicates the cell is being edited.
Spreadsheet Recording
In this tutorial, we use the Record to Spreadsheet tool to record the coordinates of a moving point along a graph of a function. We graph the function f(x) = x2, and construct point P with coordinates (a,f(a)), where a is a value on a slider. We then record the coordinates of the traces of P on the spreadsheet window. The output of this tutorial is shown in Figure 2.
If you want to follow this tutorial step-by-step, you can open the GeoGebra window in your browser by clicking here. You can view the output of this tutorial here.
Step-by-Step Instructions
| 1. Open GeoGebra select the Spreadsheet and Graphics view in the Perspectives menu. Now display the Input bar using the View menu. | |
|
|
2. To show labels of points only, click the Options menu, click Labeling, then click New Points Only. |
| 3. To graph the function, f(x) = x2 type f(x) = x^2 in the Input bar, and then press the ENTER key. | |
| 4. Now, create slider a. To create slider a, select the Slider tool and click on the Graphics View to display the Slider dialog box. | |
| 5. In the Slider dialog box, be sure that the Number option button is selected. Type a in the name box, set the minimum value to -3, the maximum value 3, and the increment to 0.5, and then close the dialog box. | |
| 6. To create point P on the graph of the function, type P = (a,f(a)) in the input box, press the ENTER key on your keyboard. Note that a is the value of your slider. | |
| |
7. Use the Move Graphics View tool to adjust the location of the Graphics view. Be sure that y = 0 up to y = 9 is visible. Use the Zoom tool if necessary. |
| |
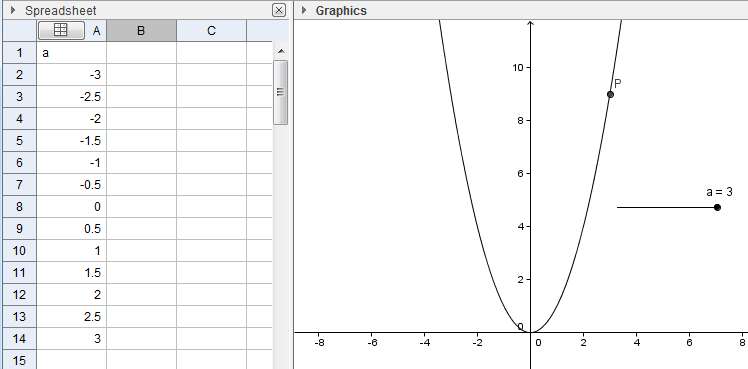
8. Set the Slider to a = -3. To record the coordinates of P in the spreadsheet, click cell A1, select the Record to Spreadsheet tool, and then Move the slider slowly from -3 up to 3. |
|
9. Without clicking anything, select the Move button and click on a blank space on the Graphics view to stop recording. After this step, your spreadsheet window should look like Figure 4. |
|
|
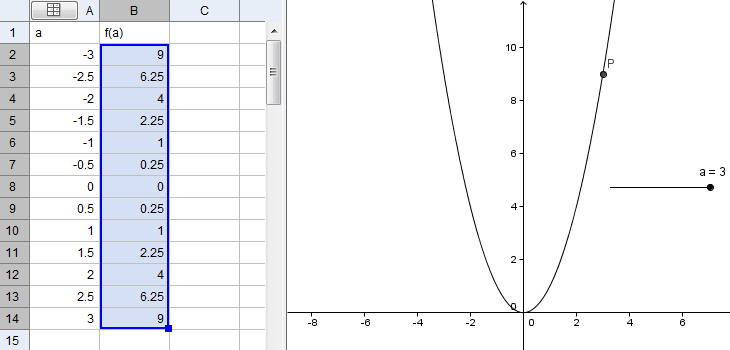
10. Next, we find the value of f(a). To do this, select cell B1 and type “f(a)”. Select B2, and then type = f(A2) and then press the ENTER key This means that you are placing the value on A2 which is 3 into f. |
|
|
11. Now, to fill out the value of f(a), select cell B2 and drag the small blue square on the lower right corner of the cell pointer all the way to B14. Your spreadsheet should look like Figure 5 after this step. |
|
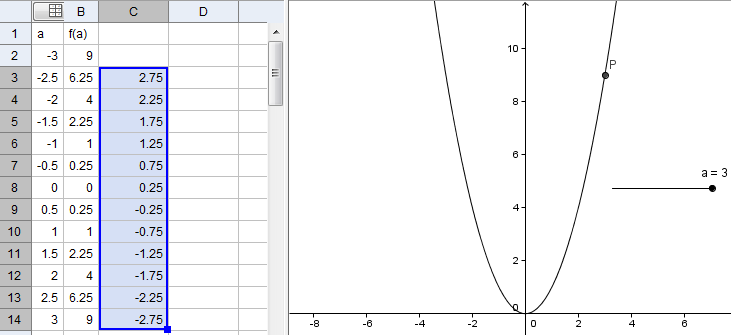
| 11. We now use the spreadsheet to show that the second difference is constant. To get the first difference, we first subtract the content of B3 from the content of B2. We place the difference in C3. To do this, click cell C3,then type = B2 – B3 and then press the ENTER key. The formula in thespreadsheet always starts with an equal sign. Note that in typing B2, you are actually telling GeoGebra to refer to the value located in cell B2. | |
|
12. We now copy cell C3 all the way to C14. To copy, drag the blue square on the lower-right corner of the cell pointer all the way down to C14. If you have done the previous steps correctly, your spreadsheet should look like the one shown in Figure 6. |
|
| |
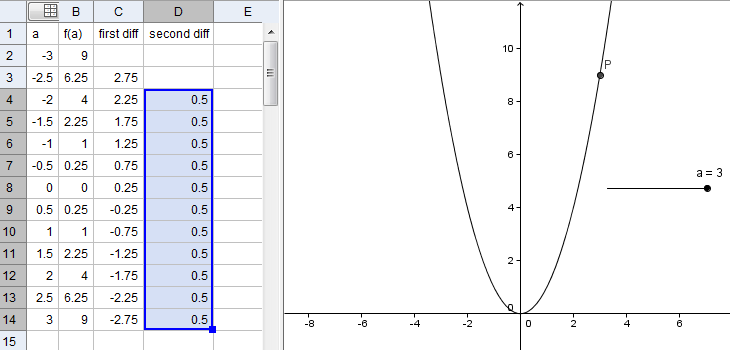
13. Now get the second difference by subtract C4 from C3 and placing the difference in D4. |
| |
14. Copy the formula from D4 all the way down to D14. Here, we have shown that if the interval between the values of a is constant, the second difference of the y-values of a quadratic equation is constant. |
Note: It is important to place double quotes on both sides of the text you want write. Typing a single letter may be misinterpreted by the spreadsheet. For example, if you type x without double quotes, the spreadsheet will read it as y = f(x) and GeoGebra will graph the said function.