GeoGebra Tutorial 25 – The Rolling Circle
This is the 25th tutorial in the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, you might want to read the GeoGebra Essentials Series.
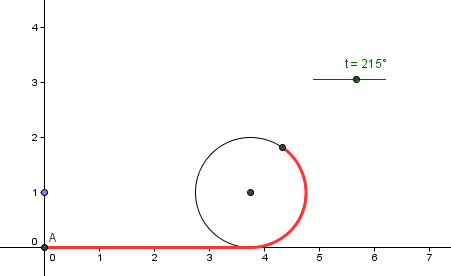
In this tutorial, we use GeoGebra in constructing a rolling circle. This way, we would be able to relate the diameter of the circle to its circumference. Moreover, this activity will reinforce the relationship between the angle and radian measure.
You can view the output of this tutorial here.
| 1. Open GeoGebra and select Algebra and Graphics from the Perspectives menu. | |
| 2. To show labels of new points, click the Options menu, click Labeling, then click New Points Only. | |
| 3. To create point A on the origin, select the Intersect Two Objects tool, click on the x-axis then click on the y-axis. | |
| 4. Create point B on the y-axis. To do this, select the New Point tool, and then click on the positive y-axis. Be sure that point B stays on the y-axis even if you drag “outside.” If not, repeat the construction. | |
| 5. Now, we create ray AB. To do this, select the Ray through Two Points tool, click point A and then click point B. | |
| 6. Next, we hide point B. To do this, right click point B, then click Show Object. | |
| 7. To be sure that we create point C on ray and not on the y-axis, we hide the Axes and create point C on the ray. Hide the axis using the Styling bar. | |
|
|
8. We now create point C on the ray. To do this, select the New Point tool and the ray. Now, show the Axes using the Styling bar.
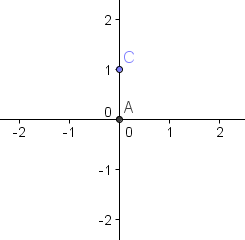 Figure 2
|
| 9. The idea of steps 1 through 8 is to ensure point C will only lie along the positive y-axis. This is because we want to use point A in the origin as “lowest point” of the circle. If we are going to use B without the ray, it can move freely along the y-axis. | |
| 10. We now create a slider |
|
| 11. In the Slider dialog box , choose the Angle option button leave the other values as is (0 to 360 degrees) and click on the Apply button. | |
| 12. We now compute for s in s = rθ, where s is the arc of the circle with radius r inscribed by angle θ. | |
| 13. We measure radius r, which is the distance between point A and point C. To measure the radius, type r = distance[A,C]. | |
| 14. We now convert the degree measure of t to radian. Type θ = (t/°)*(pi/180). The ° and the θ symbol can be found at the boxes next to the input box. Also, we divide t with ° to change convert the angle measure in degrees to number. This is because we cannot multiply the angle measure by a number. | |
| 15. We now compute for the value of s: type s = r*θ in the Input bar. You can find the symbol θ symbol in second drop down box to the right of the input box. | |
| 16. We will now construct the center point of our rolling circle which we will name P. Type P = (s,y(C)). | |
| 17. We now construct a circle with center P and radius r. To do this, click the Circle with Center and Radius, click point P and type r in the Circle with Center and Radius dialog box. Recall that r is the radius, so when you move point A, the radius length changes. | |
| 18. Select the Intersect two Objects tool, click the circle and click the x-axis to construct point D, the intersection of the said objects. We will use point D as a starting position of our rotating point. | |
| 19. To construct the rotating point, select the Rotate Object around a Point by Angle tool, click point D and click point P to display the Rotate object Around Point by Angle dialog box. | |
20. In Rotate object Around Point by Angle dialog box, replace its value with t, select the clockwise option button and click the Apply button to finish. The new constructed point should be named D’.
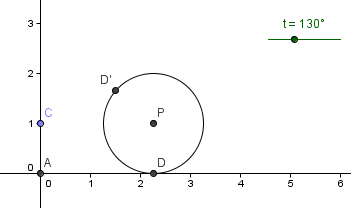 Figure 4 |
|
| 21. Move slider t back and forth. What do you observe? | |
| 22. We will now construct arc DD’, the arc to the right hand side of the diagram. To do this, select Circular Arc with center Between Two Points, click point P, click point D and then click point D’. | |
|
|
23. We will now change the color of the arc. To do this, right click arc DD’ and a dialog box will appear containing the name of Circle c and Arc d. Choose Arc d from the dialog box and then click Properties from the context menu. |
24. In the Properties dialog box, choose Color tab then choose red, or any color you want. With the dialog box still open, select the Style tab and move the Line Thickness slider to 6, then click the Close button. Your drawing should look like the Figure below.
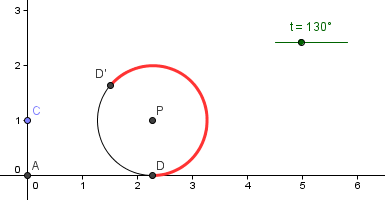 Figure 5 |
|
| 25. We want to know how far D’ has traveled along the circumference of the circle clockwise, or we want to know is how long is the non-red minor arc DD’ in Figure 5, or equivalently, how much is the circumference of the circle less arc d. Note that the name of our circle is c (see Algebra window). To do the computation, type d’ = circumference[c] – d. | |
|
|
26. Let us first hide D by right-clicking it and it and selecting Show label from the context menu. |
| 27. We now construct a segment with length d’ and one endpoint at A. To do this, click the Segment with Given Length from a Point, the click point A to display the Segment with Given Length from Point dialog box. | |
| 28. In the dialog box, type d’ as Length of the segment. GeoGebra will name the other point segment E, which coincides with point D, that we just have hiddent. | |
| 29. Next, we will copy the visual style of the red arc and to segment AE. To do it, click the Copy Visual Style tool, select the red arc, and then click segment AE. This will copy the color and thickness of the red arc. | |
|
|
30. Hide the label of point D’ by right clicking it and select Show label from the context menu. |
|
|
31. We’re almost done but we still have a problem. Move the slider to 0 degrees. You will see that segment AE is visible. But this only happens when t = 0. So, we will set a condition to show only AE when t is not equal to 0. To do this, right click segment b and select Object Properties from the dialog box. |
32. In the Object Properties dialog box, select the Advanced tab, then stype t≠0 in the Condition to Show Object box, then click the Close button.
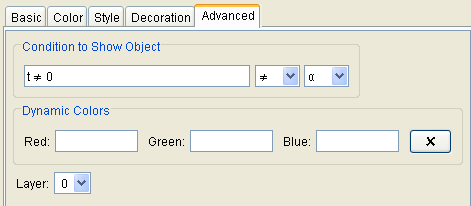 Figure 6 |
|
| 33. As an exercise, create a circle with center C and passing through point A with similar visual style as arc d. Then show it, if and only if d = 0. | |
|
|
34. Hide the labels of point P and point C. Hide Point E. |