Matchsticks, Linear Relations, and Multiple Representations
Introduction
We have mentioned the different types of functions in the Introductions to Functions post. In this post, we are going to learn about linear function and its characteristics.
To start, let us examine the problem below taken from the TIMSS 2003 released items given to Grade 10 students in more than 40 countries all over the world.
Matchsticks are arranged as shown in the figures.
If the pattern is continued, how many matchsticks would be used to make figure 10.
A. 30 B. 33 C. 36 D. 39 E. 42
The problem is too easy that even a first grade pupil would be able to answer it given enough time. Smart students would be able to easily see patterns. For example, they can relate the number of squares to the number of matchsticks. If they cannot find a pattern, the last resort would be by brute force; that is, by manually drawing the tenth figure.
Learning mathematics over the years of schooling has taught us to find solutions that are easy to understand, concise, and elegant. Drawing is a lousy and cumbersome option. Besides, what if the question asked for the number of matchsticks in figure 100? Surely, it would take us ages to be able to draw the correct figure.
The easiest way to answer the problem above without the knowledge of algebra is to use a table. To see that pattern easily, we will relate the figure number and the number of matchsticks. It is clear that the each time a figure number is added by 1, a square is added; and it is clear that in each square added, three matchsticks are added. From the table, we can see that the answer to the question above is 33.

We still have one challenge though. How many matchsticks would be used in Figure 100? Figure 200? Would making a table still be a practical solution?
As we can see, the use of table is very limited. That is why we need to devise a way how to compute for the number of matchsticks given any figure number.
Hmm… let us think for a while. From the table, it is clear that the differences between two consecutive terms, both in the figure number and the number of matchsticks are similar. The difference between the consecutive figure numbers is always 1 and the difference between the numbers of matchstick is always 3.
Figure 10 shows us 33 matchsticks, or three more than three times the figure number. Looking at the ordered pair, this observation is also true. Therefore
number of matchsticks = three times the figure number + 3
If we let y be the number of matchsticks and x be the figure number then y = 3x + 3. From the formula, it is now possible to determine the number of matchsticks given any figure number. Figure 100 will need y = 3(100) + 3 = 303 matchsticks and figure 200 will need y = 3x + 3 = 3(200) + 3 = 603.
How about Figure 1000?
The equation y = 3x + 3 is an example of a linear equation. Since there is one-to-one correspondence between x and y, the equation y = 3x + 3 also fits the definition of a function. Functions of the form y = ax + b, where a and b are real numbers is are called linear functions.
Graphing the Relationship
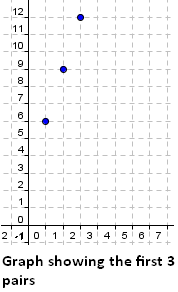
The graph of the ordered pairs (x,y) in the table above is shown in the Cartesian plane below. We can observe that the points lie on a straight line. We have said that the difference in consecutive y values is always 3 and the difference in consecutive x-values is equal to 1.
Recall that the “difference in y” over the “difference in x” is equal to the slope of the line. Therefore, the slope of the line passing through the points is equal to 3/1=3.
Graph showing the first six pairs
If we draw a line passing through the points, one good question to ask would be
“Where will the line hit y-axis?”
Using the graph, we can see that the graph hits the y-axis when x=0, since the y-axis passes through x=0.
Therefore, to find the value of y-intercept (the point on the y-axis where the graph passes through), we set x = 0 and then look for the value of y. Using the table, we can make x = 0 by subtracting 1 from the smallest x-value. Since the difference in y is constant, we also subtract 3 from y, giving us x = 0 and y = 3. Therefore the graph passes through the (0,3), the red point shown below.
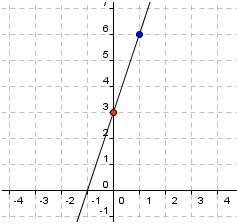
In equation form, again we just set x =0:
y= 3x + 3, y = 3(0) + 3, y = 3.
Now we see why we let x = 0 when we want to get the y-intercept of a function. In equation and table form, it is also clear that if we find the x-intercept of a graph, we just set y=0 and find the value of x.
In the linear equation y = ax + b, a is the slope. If we set x =0, then y = b. This means that b is the y-intercept. Setting y = 0, we get x = -b/a.
Teaching Note
The situation above shows how we can use a simple problem to introduce a mathematical concept. We have used the matchsticks problem to introduce linear relations. We also have introduced the different representation of functions – words, table, graph and equation. Although the discussion above is in lecture form, good questioning strategies would elicit students’ problem solving skills like searching for patterns, making conjectures, choosing appropriate solutions and multiple representations.
Read and Learn More