Introduction to Similarity
In layman’s language, we say that two objects are similar if, in some way, they share certain characteristics. For example, we can say that two flowers are similar if they have the same number of petals and they have the same color, although, they might be different flowers.

Are Buu and Patrick similar?
Mathematically, similarity is quite different. In mathematics, we say that two objects are similar if they have “the same shape, but not necessarily have the same size.”
Now what does that exactly mean?
Similarity is an enlargement or reduction of objects. A picture, for instance, may be enlarged or reduced in two ways. One way is stretching/shrinking it in proportion, and the other stretching/shrinking it horizontally or vertically. When we say enlargement/reduction by proportion, we mean that if we want to increase/decrease the length by any percentage, we also increase/decrease the width by a similar percentage.
We can easily see that enlargement/reduction of pictures not in disproportion as shown below gives us a somewhat stretched picture. The second and the third picture in the first figure below are stretched horizontally and vertically, respectively.

This means that if we want to preserve the appearance of our picture, we must enlarge or reduce it in proportion. The second figure is the proportional enlargement of the original photo.
In mathematics, we can only say that two objects are similar if their measurements are proportional.

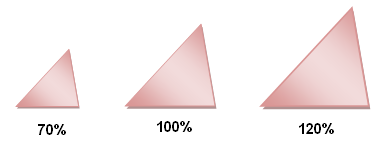
Using our word processor or any graphics software, we can understand similarity by zooming in or zooming out a particular drawing or picture. Take for example the triangles below. The second drawing in the figure was the original figure drawn, the first figure was zoomed out to 70 percent, and the third figure is zoomed in by 120 percent. The three triangles are similar because they have the same shape (we did not modify the shape of the triangle), but not necessarily of the same size.
Now that you have the intuitive notion of similarity, in the next post, we are going to discuss the properties of similar triangles.
Photo Credits: Buu vs Patrick (unknown source), Kisha Chelsea (my Goddaughter).