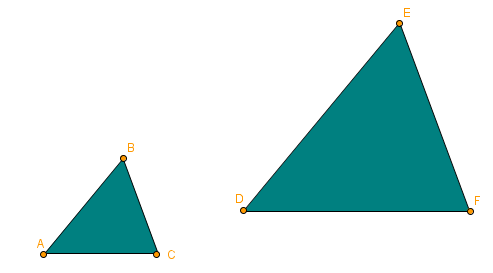Properties of Similar Triangles Part 1
This is the second part of the Triangle Similarity Series. The first part is Introduction to Similarity.
In Introduction to Similarity, we have learned that similar objects have the same shape, but not necessarily have the same size. We drew a triangle using a graphics software zoomed it in and zoomed it out producing similar triangles.

Are Buu and Patrick 'similar'?
Zooming did not change the shape of the object. In effect, the measure of the interior angles of a triangle did not change.
In this post, we are going to explore more properties of similar triangles. We are going to perform another activity. Follow the instructions below and answer the questions.
Instructions
1.) Use a graphics to draw a triangle. Be sure to zoom in to 100 percent.
2.) Take a photo of the triangle. Use the Print Screen key on your keyboard on a PC (or Apple Command key + Shift + 3 on a Mac) to grab the picture of the triangle, crop it so that the picture fits the canvas, and save the file as triangle1 in png or jpg format. You can also screenshot software such as Jing.
3.) Adjust the zoom to 200 percent and repeat 2. Save it as triangle2 in png or jpg format.
4.) We now use GeoGebra to explore the properties of the two triangles. Use the GeoGebra Insert Image button to import both triangles in the GeoGebra graphics view (drawing pad). Using the Point tool, place points on all the vertices of the triangles. Your figure should look like the figure below.
5.) Connect the corresponding vertices ( A to D, B to E, and C to F). What do you observe? Some students will observe that the lines meet, some won’t because of the slight error in placement of the points.
6.) We have said that zooming in or out does not change the shape of the triangle. Therefore, the corresponding angles of similar triangles are congruent. In the figure above, A corresponds to D, B corresponds to E, and C corresponds to F. Therefore, A is congruent to D, B is congruent to E, and C is congruent to F.
7.) Using the Angle, Area, and Distance tools of GeoGebra, investigate the relationships between the two triangles. What can you say about the relationship between the side lengths and area of the two triangles?
8.) Take note of your observations and make conjectures about them. Try proving your conjectures.
We will continue discussing your observations in the next part of this series.