Corresponding Angles of Similar Objects

In this post, one property of similar objects. In the previous article, we have discussed that if we want to preserve the appearance of our picture or object (that is without being stretched), we will have to enlarge or reduce it with the same proportion. That means that if we double the width of our picture, then we will also have to double the length.  We have done this using the two triangles as shown below.  We made sure that if we pair the sides of the two triangles, in each pair, the length of the side of the larger triangle is always twice the length of its pair.  This means that the length of DF is twice the length AC, the length of DE is twice AB, and the length of EF is twice the length of BC.

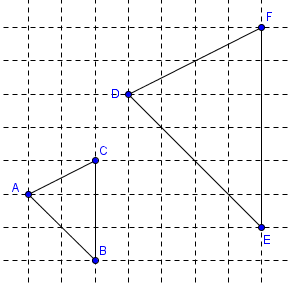
We will call the pair of sides that we have mentioned above corresponding sides. We can say that AB corresponds to DE, BC corresponds to EF and AC corresponds to DF. We will also identify the corresponding angles. We can also say that angle A corresponds to angle D, angle B corresponds to angle D, and angle C corresponds to angle E.

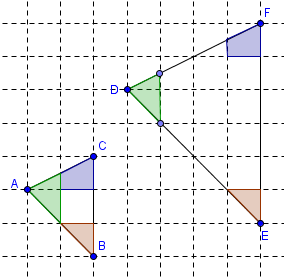
One thing that we can observe also is that the corresponding angles are congruent. This can easily be seen in the figure below. From here, we can hypothesize that corresponding angles of similar objects are congruent.  We can also conjecture that if two objects are similar, their corresponding sides are proportional and their corresponding angles are congruent.

In the next post, we are going to discuss two things. First, we will construct a triangle by copying the angles, and see if the sides are still proportional.