Platonic Solids: Why only five of them?

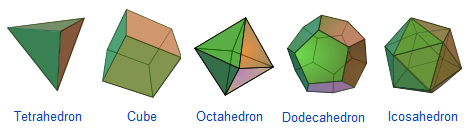
Regular polygons are polygons with congruent sides and congruent interior angles.  In three dimensions, the equivalent of regular polygons are regular polyhedra — solids whose faces are congruent regular polygons.  The most common regular polyhedron is the cube whose faces are congruent squares.  The other regular polyhedra are shown below.

Regular polyhedra are also known as Platonic solids — named after the Greek philosopher and mathematician Plato. The Greeks studied Platonic solids extensively, and they even associated them with the four classic elements: cube for earth, octahedron for air, icosahedron for water, and tetrahedron for fire.

There Are Only Five Platonic Solids

Interestingly, even though  we can create infinitely many regular polygons, there are only five regular polyhedra. And the proof is fairly easy. Before we discuss the proof, let us familiarize ourselves with the different terms which we will use in the proof.

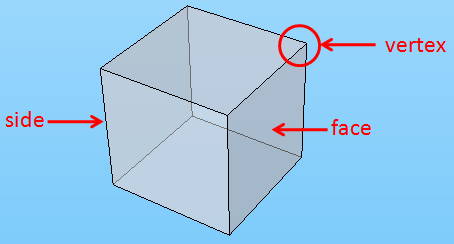
In the following discussion, vertex will refer to the corner of a Platonic solid, face will refer to the regular polygons that make up the solid, and side (edges in 3D) will refer the side of the polygon.

The Proof

Let be the number of sides of a regular polygon on a Platonic solid, and be the number of polygons meeting at each vertex. Let us represent each regular polygon with . For example, a cube maybe represented as since the faces of a cube (the squares) have four sides, and three squares meet at a cube’s vertex.

Notice that the interior angles of the regular polygon can be expressed as (recall sum of interior angles of a polygon) which is equal to . Since is convex, the sum of the angles at one vertex is less than 360 degrees (Can you see why?). Therefore, we can setup the following inequality:

It is clear that the values of and must be both greater  than (Why?). Now, if , the only possible values for are and .  These values give us the solids (the tetrahedron), (the octahedron) and (the icosahedron). If , we only have , (the cube). If , then, we have only , (the dodecahedron). Now, cannot be greater than since it will not satisfy the inequality.

Therefore, the only platonic solids are  , , , and . Hence, there are only five platonic solids, and we are done with our proof.

***

Photo Credit: Wikipedia