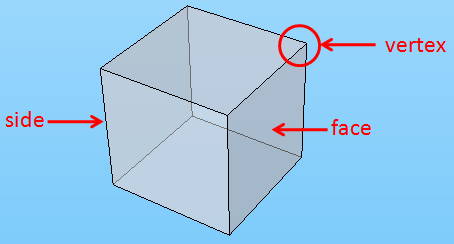
Regular Tessellations: Why only three of them?
In Tessellations: The Mathematics of Tiling post, we have learned that there are only three regular polygons that can tessellate the plane: squares, equilateral triangles, and regular hexagons. In Figure 1, we can see why this is so. The angle sum of the interior angles of the regular polygons meeting at a point add up to 360 degrees.
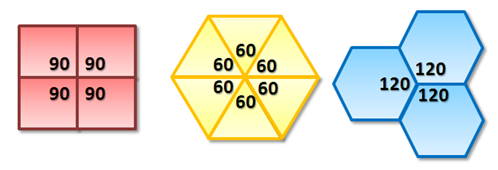
Figure 1 – Tessellating regular polygons.
Looking at the other regular polygons as shown in Figure 2, we can see clearly why the polygons cannot tessellate. The sums of the interior angles are either greater than or less than 360 degrees. » Read more