Regular Tessellations: Why only three of them?
In Tessellations: The Mathematics of Tiling post, we have learned that there are only three regular polygons that can tessellate the plane: squares, equilateral triangles, and regular hexagons. In Figure 1, we can see why this is so. The angle sum of the interior angles of the regular polygons meeting at a point add up to 360 degrees.
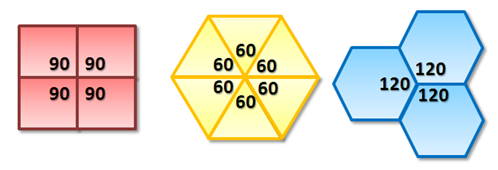
Figure 1 – Tessellating regular polygons.
Looking at the other regular polygons as shown in Figure 2, we can see clearly why the polygons cannot tessellate. The sums of the interior angles are either greater than or less than 360 degrees.
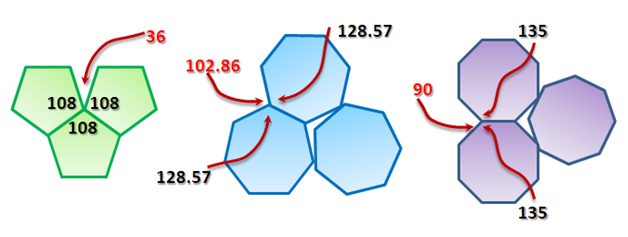
Figure 2 – Non-tessellating regular polygons.
In this post, we are going to show algebraically that there are only 3 regular tessellations. We will use the notation , similar to what we have used in the proof that there are only five platonic solids, to represent the polygons meeting at a point where
is the number of sides and
is the number of vertices. Using this notation, the triangular tessellation can be represented as
since a triangle has 3 sides and 6 vertices meet at a point.
In the proof, as shown in Figure 1, we are going to show that the product of the measure of the interior angle of a regular polygon multiplied by the number of vertices meeting at a point is equal to 360 degrees.
Theorem: There are only three regular tessellations: equilateral triangles, squares, and regular hexagons.
Proof:
The angle sum of a polygon with sides is
. This means that each interior angle of a regular polygon measures
. The number of polygons meeting at a point is
. The product is therefore
which simplifies to . Using Simon’s Favorite Factoring Trick, we add
to both sides giving us
. Factoring and simplifying, we have
, which is equivalent to
. Observe that the only possible values for
are
(squares),
(regular hexagons), or
(equilateral triangles). This means that these are the only regular tessellations possible which is what we want to prove.