Addition of Coordinates
If we have two points, what will happen if we add their coordinates? If point has coordinates
and point
has coordinates
, then
. It seems that there is nothing special about these points, but let us look at their position in the Cartesian coordinates.
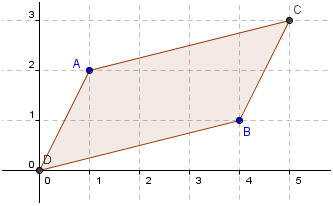
Notice that if we add another point on the origin, the four points form a parallelogram. Now the question is, is this always the case? Try plotting two points and add their coordinates several times and see if the four points form a parallelogram. What do you observe?
To test further our observation above, we use GeoGebra to plot the two points and automatically produce the ‘sum point.’
Instructions
- Open GeoGebra
- To plot the points, type the following equations in the input bar and then press the Enter/Return key on the keyboard after each equation:
,
,
.
- To create the fourth point
, click the Intersect Two Object tools, click the x-axis, and then click the y-axis.
- To draw the quadrilateral, click the Polygon tool, and then click points
in that order.
- Now move point
or
. Is the quadrilateral always a parallelogram? What conjecture can be made from your observations?
We now prove our conjecture above.
Theorem: If you add the coordinates of two points and
, and construct another point
whose coordinates are the sum of the coordinates of points
and
, then three points form a parallelogram containing the origin as its fourth vertex.
Proof: Let the coordinates of and
be
and
respectively. Then the coordinates of
. Let
be the point at the origin. We have to show that
is a parallelogram.
There are several ways to prove this, but it is sufficient to show that the opposite sides of the are parallel; that is,
is parallel to
and
is parallel
.
We now compute the slopes of each side of the parallelogram.
As we can see, the slopes of and
are equal, which means that they are parallel. Also, the slopes of
and
are equal, which means that they are also parallel. Therefore,
is a parallelogram.
Note that the parallelogram method above can also represent addition of vectors.