Vectors, Parallelograms, and Commutativity
Basics of Vectors
Scalar quantities are quantities specified by magnitude. Mass, area, density are examples of scalar quantities. There are quantities that have both magnitude and direction. For example, when we say 2 kilometers east, 2 kilometers is our magnitude and east is our direction. Quantities with both magnitude and direction are called vectors.
In mathematics, vectors are usually represented by a directed line segment. The arrow of the directed segment is called its head, and the other end is called its foot.
Comparing Vectors
Two vectors are said to be equal if they have the same length and the same direction. Plainly speaking, if we look at the geometric representation of vectors, equal vectors have the “same slope and the same direction (of the arrow).” In Figure 1, it is clear that there only two equal vectors – vector u and vector v.
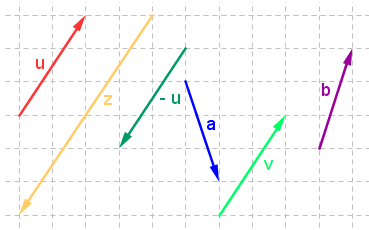
Figure 1
The negative of a vector is the vector equal in length to a certain vector, but with opposite direction. For instance, in Figure 1, – u and u are negative of each other and vector u is also the negative of vector v.
Experimenting Coordinates
We leave vectors for while and amuse ourselves with the points in the coordinate plane. What if we add the coordinates of two points? What do you think will happen?
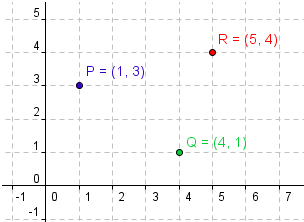
Let’s give a try. Suppose we have two points, say P (1,3)and Q (4,1). What is the geometric interpretation of P + Q = (1 + 4, 3+ 1) = (5,4) in the coordinate plane? Let us assign the name R to the “sum point” (5, 4) as shown in Figure 2.
What do you observe about the three points shown in Figure 2? Is there anything special about them?
Before continuing reading, try to explore the applet (click the picture below to open the applet) by moving points P and Q. Observe what happens to the sum point as you move P and Q.
Going back to vectors
If we will consider the three points as heads of vectors with foot O at the origin, then we have three vectors OP, OQ and OR (or vectors u, v and w) as shown in Figure 3. We know that R is our sum point, so it is clear that the OR is the sum of vectors OP and OQ. Therefore we can form the equation OP + PQ = OR*, or equivalently u + v = w.

Figure 3
Earlier we said that two vectors are equal if they have the same direction and the same length. If we move a vector without changing its direction (that is if we translate it) then it doesn’t change its value. If we move OP such that its foot is at the head of OQ (Figure 4), we form a triangle OQR where OQ + QR = OR.
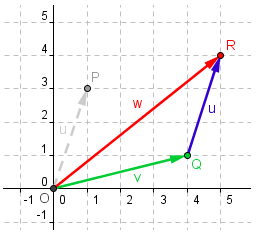
Figure 4
Using this principle, we can conclude that if we have two vectors OQand QR, then its sum is equal to the vector OR.
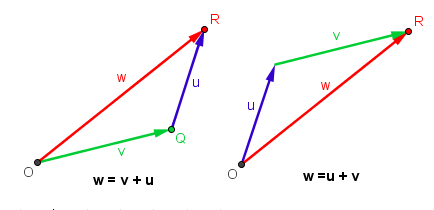
Figure 5
It is also clear that the order of the vectors do not matter. For instance, instead of moving u to the right (Figure 5-1), we can move v to the “top part” (Figure 5-2) and still our sum is OR. From here, we can also conclude that addition of vectors is commutative. That is, if we have vectors u and v, then u + v = v + u.
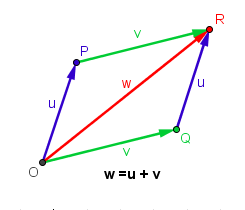
Figure 6
The geometric interpretation of this property is the parallelogram formed as shown in Figure 6. That is, if we connect the four points — three vector heads and the origin — we will form a parallelogram.
—
*The addend vectors are usually called component vectors, while the sum vector is called resultant vector.