The Geometry of Commutativity
One of the elementary observations about real numbers is that if we add the two numbers, regarding of the order, their sum is unique. We know that 4 + 3 = 3 + 4. This property is also the same when we multiply. If we have two numbers, regarding of the order, their product is also unique. For example, 6 x 3 = 3 x 6.
In general if we have real numbers a and b, we have a + b is always equal to b + a. Also, if we have real numbers c and d, c x d is always equal to d x c. These are called the commutative property of addition and multiplication, two of the axioms of algebra.
Although axioms, as we have discussed, are statements that we accept without proof, some axioms can be explained intuitively. In this post, we are going to discuss the two axioms mentioned above intuitively using geometric representations.
The geometry of a + b
One way of understanding why a + b is always equal to b + a is by representing the two numbers as lengths. For instance, we can represent the addition of integers above (4+3 = 3 + 4) as the sum of the lengths of two segments. In geometric representation, reversing the order of the numbers in the operation is just like rotating the segment 180 degrees about the center as shown below. Of course, rotating the segment way will never change its length.
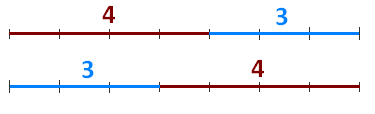
Now, since that we can substitute any positive numbers to a and b we are sure that the commutative property is true for all positive numbers. » Read more