Vectors, Parallelograms, and Commutativity
Basics of Vectors
Scalar quantities are quantities specified by magnitude. Mass, area, density are examples of scalar quantities. There are quantities that have both magnitude and direction. For example, when we say 2 kilometers east, 2 kilometers is our magnitude and east is our direction. Quantities with both magnitude and direction are called vectors.
In mathematics, vectors are usually represented by a directed line segment. The arrow of the directed segment is called its head, and the other end is called its foot.
Comparing Vectors
Two vectors are said to be equal if they have the same length and the same direction. Plainly speaking, if we look at the geometric representation of vectors, equal vectors have the “same slope and the same direction (of the arrow).” In Figure 1, it is clear that there only two equal vectors – vector u and vector v.
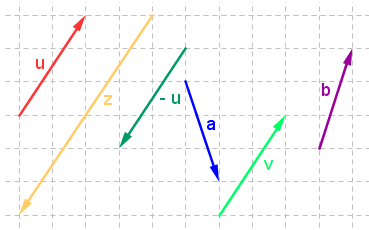
Figure 1
The negative of a vector is the vector equal in length to a certain vector, but with opposite direction. For instance, in Figure 1, – u and u are negative of each other and vector u is also the negative of vector v. » Read more