Geometer’s Sketchpad Essentials 3 – Constructing an Incircle
This is the third part of the Geometer’s Sketchpad Essentials Series. In this tutorial, we are going to construct the incircle of a triangle. In doing so, we are going to learn how to use the Compass tool and construct Angle bisectors.
Step by Step Instructions
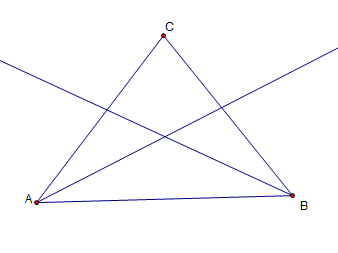
1.) Using the Segment tool, construct a triangle.
2.) Select the Text tool and click each vertex to reveal their names. GSP will name the triangle ABC.
3.) To construct the angle bisector of angle A, deselect all the objects, and then click the vertices in the following order: B, A, C (or C, A, B).
4.) Next, click the Construct menu from the menu bar and choose Angle Bisector. This will produce a ray bisecting angle A. Now, construct the the angle bisector for angle B.
5.) To intersect the two rays, deselect all the objects, click the two rays, and choose Intersection from the Construct menu. The intersection of the two rays will be the center of our circle.
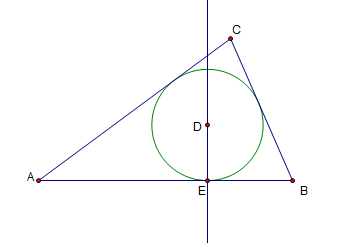
6.) Now, hide the bisector by clicking the Hide Bisectors from the Display menu, and use the Text tool to display the name of the intersection point. This is named D.
7.) The incircle is tangent to the sides of the triangle. To create the point of tangency, we create a point on one of the sides that is perpendicular to D (Why?). To do this, select segment AB (be sure not to include points A and B), select point D, click the Construct menu, and then click Perpendicular Line.
8.) Select the perpendicular line and segment AB, and choose Intersection from the Construct menu to construct the intersection. Use the Text tool and name the intersection E.
9.) To construct the incircle, click the Compass tool, click point D, and then click point E.
10.) Now, hide the perpendicular line passing through D by selecting it, and then clicking Hide Perpendicular Line from the Display menu.
11.) Now, move the vertices of the triangle. What do you observe?
The circle with center us inscribed to triangle ABC. This circle is called the incircle of triangle ABC.