When do mathematical definitions matter?
In the movie Hanna, Hanna was a 16 year old girl who grew in the wilderness of Finland. Since two years old, she never had contact with the real world and modern technology. Hanna learned about the world from Erik, his adopted father, and by reading books. In one of the father-daughter conversations, Hannah asked about music. Their conversation was as follows.
Erik: Music is a combination of sounds with a view of beauty to form.
Hanna: But how does it feel?
Erik: Good. It feels good. It’s, uh,nice.
Hanna: Tell me properly. Can you play music?
Erik: Your mother could. She used to sing very well.
Hanna: I’d like to hear it for myself.
Hanna probably feels the way students feel when we define an unfamiliar concept. To students who are mathematically matured, definitions at the beginning of the lesson are probably understood, but for those who are just learning the basic concepts, it might be a little vague. Imagine a teacher saying that a function is a correspondence between two sets A and B, where each element in A has exactly one and only one corresponding element in B to students who have no prior experience of the said relationship.
In several middle school classes that I have observed, students are bombarded with definitions at the beginning of the lesson without relating to context. I remember one class having all definitions in one-hour lesson: definition of the parts of triangles angles, vertices, sides, altitudes, medians, types of triangles by angle, types of triangle by sides, etc. Do students really need to learn all those definitions in one lesson?
Although it may not always be applicable, I believe most definitions should come at the last part of the lesson, or should be derived from contexts, especially in elementary and middle school mathematics. You don’t say to a 7-year old kid who has not seen a dog that a dog is “any carnivore of the dog family Canidae, having prominent canine teeth, a long and slender muzzle, a deep-chested muscular body, a bushy tale and large, erect ears (Dictionary.com).” Instead, you show him a dog. Later, he would distinguish what a dog is, and later he would be able to describe a dog in his own words.
One sample lesson where definition is at the end is the Introduction to the Concept of Function which I have written more than year ago (I have tried out this lesson in actual class) and although, there was no comparative study done, there was obviously more thinking done in that kind of strategy than the one I had used before (defining what a function is first).
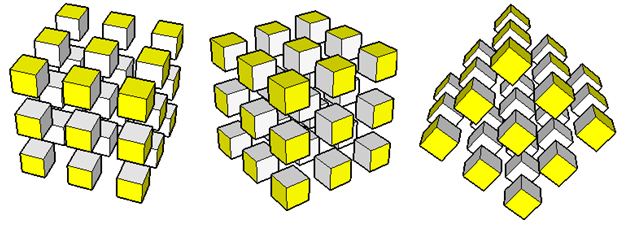
That lesson was about the classic painted cube problem (see link above for details). Students were asked to find the number of cubes whose faces were painted: no painted face, 1 painted face, 2 painted faces, and 3 painted faces. Then they were asked to find a formula that would determine the number of painted faces given any cube size. The teacher should note that for each side (starting from 2), there is a corresponding number of painted faces (in fact one-to-one correspondence), and from this correspondence comes in the introduction of the concept of function — the definition.
There are a lot of theories and studies done in mathematics teaching, but I think, the best way of teaching mathematics is the one that makes students think the most.