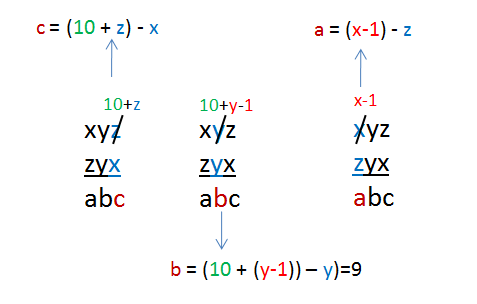The mystery of 495 explained
In yesterday’s post, we chose a three digit positive integer and we arranged the digits in ascending and descending order forming the largest and the smallest integer that can be formed using the three digits. We subtracted the smaller integer from the larger, and repeated the process several times. We ended up with 495. We tried other integers and repeated the process, and they all ended up with 495. In this post, we are going to discuss the reason behind our observation.
Let’s take the first example in yesterday’s post. We chose 592. Arranging the numbers in descending and ascending order, we got 259 and 952. Subtracting the numbers, we got 693.
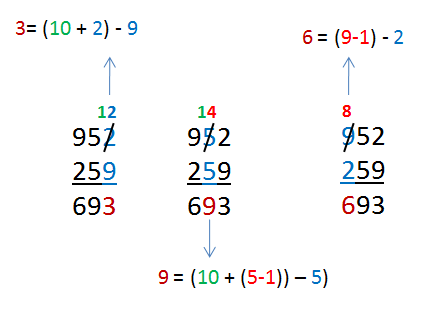
Let us examine closely what happens when we subtract the numbers with rearranged digits (examine the figure above):
- In the ones’ place, the subtrahend is always greater than the minuend (Why?).
- In the tens’ place, the difference is always 9 (Why?).
- In the hundreds’ place, we always subtract 1 from the hundred’s digit of the minuend, before subtracting the hundreds’ digit.
The generalization of the subtraction process is shown below. If the digits of the numbers are represented by x, y, and z, where x>y>z (strictly speaking, at most two numbers can be equal), then the largest number that we can form from this digits is xyz and the smallest is zyx. If abc is the difference, then the following relationships hold (can you see why?):
c = 10 + z –x
b = 9
a = x – 1 – z
From the equations above, we can also conclude that a + c = 9. This means that the difference is of the form a9c where a + c = 9. This only gives us ten numbers: 099, 198, 297, 396, 495, 594, 693, 792, 891, and 990. Notice that these numbers are all multiples of 99, and, manually, we can check that all these numbers lead to 495. Note that we have already shown the integers in red led to 495 in the previous post, so we only have to verify the remaining four integers.
How about other numbers?
We only have 10 numbers above, so how do we show that any 3-digit number chosen will end up with 495?
In general, any 3-digit number with digits xyz, where x>y>z, is of the form 100x + 10y + z. The smaller number is of the form 100z + 10y + x. Subtracting, we have 99(x–z) which means that the difference of any two digit numbers satisfying the conditions above is a multiple of 99. But all the three digit numbers that are multiples of 99 are the ten numbers listed above. Therefore, repeating the process above will eventually lead to 495 for any three digit number. That explains the mystery behind 495.