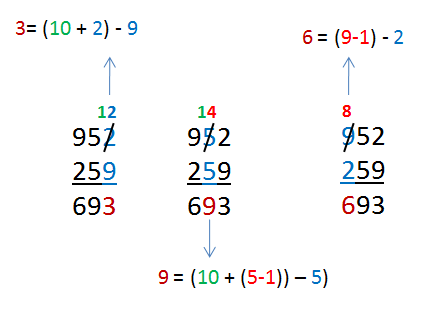
The Kaprekar constant 6174
In the mysterious 495, (1) we chose any 3-digit number, (2) arranged the digits in decreasing order forming the largest integer, (3) arranged the digit in increasing order forming the smallest integer, and (4) subtracted the smaller from the larger. Each time a difference is obtained, we repeated steps 2-4 several times and we ended up having 495. We explained the mystery behind this ‘phenomenon’ and we were quite fascinated.
In this post, we examine the 4-digit Kaprekar constant. That is, if the digits of a 4-digit number are not all equal, there is a certain number that we will end up with if we repeat the enumerated process above. Let’s have an example. » Read more