The Golden Ratio

High School Geometry, High School Mathematics

Problem: Find point P on segment AB such that AP:PB = AB:AP.

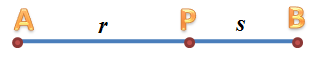
Solution:

If we let r be the length of AP and s be the length of PB, then the ratio above can be written as

\displaystyle\frac{r}{s} =\frac{r+s}{r}

Simplifying the equation we have r^2 = rs + s^2 which is equivalent to r^2-rs - s^2, a quadratic equation in r. So, we solve for r using the quadratic formula with a = 1, b = s and c = -s^2:

r = \displaystyle\frac{-b \pm \sqrt{b^2-4ac}}{2a} = \frac{-s \pm \sqrt{s^2-4(1)(-s^2)}}{2(10)}.

Simplifying this gives us r = \frac{s + s\sqrt{5}}{2}. Dividing both sides by s, we have

\displaystyle\frac{r}{s} = \frac{1 + \sqrt{5}}{2} \approx 1.61803398874989.

The ratio that given above is called the Golden Ratio.  The Golden Ratio seems to be an ordinary irrational number, but it was extensively used in ancient constructions.

Many ancient mathematicians, especially the Greeks, deemed anything that has a property of a Golden ratio somehow divine. In fact, they have integrated in in their architecture. Many proportions of the Parthenon, for instance, are said to exhibit the Golden Ratio.

The video below shows some facts (and fiction) about the Golden Ratio.

8 comments , ,

Leave a Reply