The Golden Ratio
Problem: Find point on segment
such that AP:PB = AB:AP.
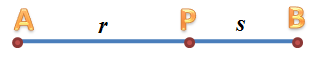
Solution:
If we let be the length of
and
be the length of
, then the ratio above can be written as
Simplifying the equation we have which is equivalent to
, a quadratic equation in
. So, we solve for r using the quadratic formula with
,
and
:
.
Simplifying this gives us . Dividing both sides by s, we have