Divisibility by 9

This is the 8th part of the Divisibility Rules Series.  In this post, we discuss divisibility by 9.

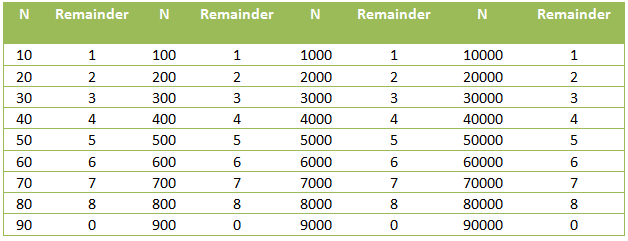
When 10 is divided by 9, it gives a remainder of 1 since 10 = 9 + 1. Also, 100 divided by 9 gives a remainder of 1 since 100 = 99 + 1. Further, 1000 gives a remainder of 1 when divided by 9 since it can be expressed as 999 + 1.  From the pattern, we can see that powers of 10 give a remainder of 1 when divided by 9 since they can be expressed as 999…9 + 1.

In addition, observe from the table that 20 divided by 9 is equal to 2, and 300 divided by 9 = 3, 5000 divided by 9 = 5. We can see that a positive integer n less than 9 multiplied by a power of 10 gives a remainder of n when divided by 9. Now since 3465 can be expressed as 3000 + 4000 + 60 + 5 = 3(10³) + 4(10²) + 6(10¹) + 5(10⁰), we can use the expanded form to determine divisibility by 9. For example,  in the second table, the  remainders of the expansion are 3, 4, 6, and 5. We now take the sum of these remainders and see if they are divisible by 9.

The process above is the same as the following analogy.  If we have 3(10)³ apples we place 9 apples in each box. For every 10³ = 1000, we have 1 remaining apple. Since we have three 1000s, that gives us three remaining apples. This is the same with the other columns 4(10)² leaves us 4 apples, 6(10¹) leaves us 6 apples, and 5(10⁰) leaves us 5 apples.  That means that we have 3 + 4 + 6 + 5 = 18 apples left.  But we know that these apples can still be placed into two boxes each of which containing 9 apples. Therefore, we can box the apples into 9’s without remainders. Therefore, 3465 is divisible by 9.

Using the apple analogy and the observation above, we can conclude that we can determine if the number is divisible by 9 by adding the digits. If the sum of its digit is divisible by 9, it is divisible by 9, otherwise it is not.

Let’s have another example. Is 8729 divisible by 9?

Doing steps 1-3, we conclude that 8729 is not divisibly by 9 since the sum of its digit is 17 and 17 is not divisible by 9. Note that 9 in the ones digit of 8729 will not matter when dividing by 9 since it gives a remainder of 0.

Summary

• The number  10ⁿ/9 gives a remainder of 1 for all positive integer n.
• a(10ⁿ) divided by 9 is equal to a  (a is a positive integer less than 9, and n is any positive integer)
• A number is divisible by 9 if the sum of its digits is divisible by 9.