divisibility rules Archives - Math and Multimedia

Divisibility by 9

April 19, 2012 GB High School Mathematics, High School Number Theory

This is the 8th part of the Divisibility Rules Series. In this post, we discuss divisibility by 9.

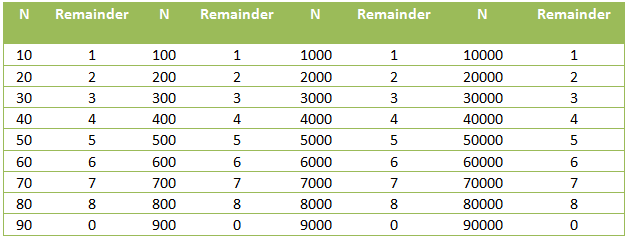
When 10 is divided by 9, it gives a remainder of 1 since 10 = 9 + 1. Also, 100 divided by 9 gives a remainder of 1 since 100 = 99 + 1. Further, 1000 gives a remainder of 1 when divided by 9 since it can be expressed as 999 + 1. From the pattern, we can see that powers of 10 give a remainder of 1 when divided by 9 since they can be expressed as 999…9 + 1.

In addition, observe from the table that 20 divided by 9 is equal to 2, and 300 divided by 9 = 3, 5000 divided by 9 = 5. We can see that a positive integer n less than 9 multiplied by a power of 10 gives a remainder of n when divided by 9. Now since 3465 can be expressed as 3000 + 4000 + 60 + 5 = 3(10³) + 4(10²) + 6(10¹) + 5(10⁰), we can use the expanded form to determine divisibility by 9. For example, in the second table, the remainders of the expansion are 3, 4, 6, and 5. We now take the sum of these remainders and see if they are divisible by 9. » Read more

One comment divisibility by 9, divisibility rules, divisibility rules series, divisibility tests

Divisibility by 8

March 3, 2012 GB High School Number Theory

This is the seventh post in the Divisibility Rules Series. In this post, we will discuss divisibility by 8.

A number is divisible by $8$ if the last three digits is divisible by $8$ . For example, $25816$ is divisible by $8$ since $816$ is divisible by 8. On the other hand, $5780$ is not divisible by $8$ since $780$ is not divisible by $8$ . Why is this so?

Let us start with $25 816$ . First, we know that $1000$ is divisible by $8$ . Therefore, $2000$ , $3000$ , $4000$ , and all multiples of $1000$ are divisible by $8$ . Since $25 816 = 25000 + 816$ and $25 000$ is divisible by $8$ , we just have examine the last three digits. Notice that this is similar to $5780$ . Since $5780 = 5000 + 780$ , and $5000$ is divisible by $8$ , we are sure that it is not divisible by $8$ since the last three digits is not divisible by $8$ .

This observation can be generalized because all numbers greater than $1000$ can be expressed as multiple of 1000 + three-digit number (the hundreds, tens, and ones). Since all multiples of $1000$ are divisible by $8$ , we just have to examine the divisibility of the last three digit number.

Of course this observation is also similar with negative numbers. All negative numbers less than $-1000$ can can be expressed as multiple of -1000 + three-digit negative number.

2 comments divisibility by 8, divisibility rules, divisibility test

Divisibility by 7 and Its Proof

February 29, 2012 GB High School Mathematics, High School Number Theory

This is the 6th post in the Divisibility Rules Series. In this post, we discuss divisibility by 7.

Simple steps are needed to check if a number is divisible by 7. First, multiply the rightmost (unit) digit by 2, and then subtract the product from the remaining digits. If the difference is divisible by 7, then the number is divisible by 7.

Example 1: Is 623 divisible by 7?

3 x 2 = 6
62 – 6 = 56
56 is divisible by 7, so 623 is divisible by 7.

If after the process above, the number is still large, and it is difficult if to know if it is divisible by 7, the steps can be repeated. We take the difference as the new number, we multiply the rightmost digit by 2, and then subtract from the remaining digits.

Example 2: Is 3423 divisible by 7?

3 x 2 = 6
342 – 6 = 336

We repeat the process for 336. We multiply 6 by 2 and then subtract it from 33.

6 x 2 = 12
33 – 12 = 21
21 is divisible by 7, so 3423 is divisible by 7.

Note that if the number is still large, this process can be repeated over and over again, until it is possible to determine if the remaining digits is divisible by 7. » Read more

9 comments divisibility by 7, divisibility by 7 proof, divisibility rules, divisibility rules 1-12, divisibility test

1 2 3 »