Counting the Number of Squares on a Chess Board
Chess is one good source of mathematical problems and puzzles. In this post, we discuss one of the most basic problems in chess: Counting the number of squares on the chessboard.
How many squares are there in a standard chessboard measuring 8 by 8 units?
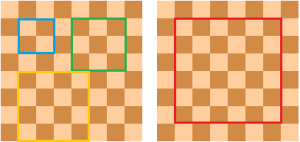
The answer is not 64 because there are larger squares that can be formed using the smallest squares as shown above. If we let the side length of the smallest squares be equal to 1 unit, then we can also count the squares with dimensions 2 by 2, 3 by 3, all the way up to 8 by 8 units. The 64 squares are only those measuring 1 by 1. Now, our problem is to count the larger squares systematically.
To count the 2 by 2 squares, we create a 2 by 2 square on the upper left corner (we call this the starting position) as shown in the leftmost diagram in the next figure. Notice that we can move the square to the right 6 times, which means that we have 7 squares from the starting position all the way to the right. In addition, we can also move the square downward 6 times which means that he have 7 squares from the starting position all the way down. Therefore, we have 49 squares with side length 2 units. (Can you see why?).
This process can also be done using a 3 by 3 square and larger squares. We can create six 3 by 3 squares from the starting position above all the way to the right and six 3 by 3 squares from the starting position all the way down. So, we have 36 squares.
Going further, we can easily see a pattern; we just have to add the square of numbers from 8 down to 1 (or 1 up to 8) as shown in the table below. That is,
.
It is clear that the process above can be extended to a square board of any size. For instance, if we want to find the number of squares on a 10 by 10 chessboard, we have to add the squares of positive integers from 1 to 10. In general, the number of squares on an by
chessboard is
.
In the next post in this series, we find an equivalent to the sum of square numbers.