Proof of the Sum of Square Numbers
In the first part of this series, we have counted the number of squares on a chessboard, and we have discovered that it is equal to the sum of the squares of the first 8 positive integers. The numbers ,
,
and so on are called square numbers.
This method can be generalized to compute for the number of squares on larger square boards. If the measure of a board is , then the number of squares on it is
.
In this post, we find an equivalent to the preceding expression using “proof without words” since adding lots of numbers is very cumbersome. For example, it is very difficult to count the number of squares in a board without using a computer.
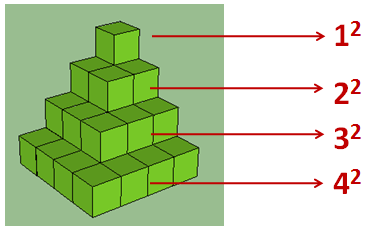
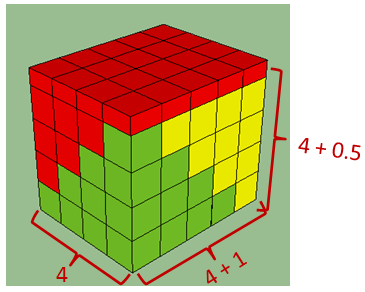
To look for the equivalent expression, we use a quite different approach. First, we create cubes (I used Google Sketchup) and form prisms with square base sharing the same corner. We stack them together as shown in Figure 1. From top to bottom, we have prisms with square base made up of 1, 4, 9, and 16 cubes.
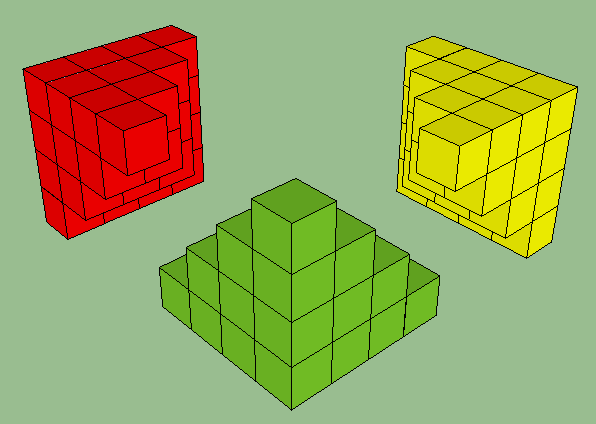
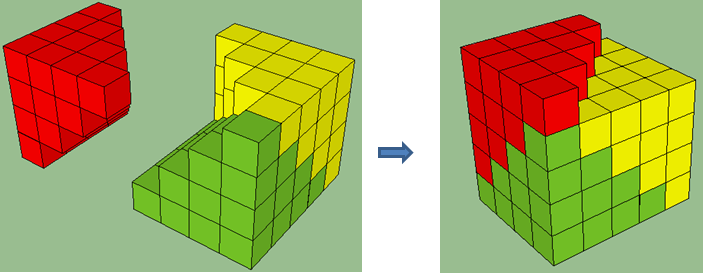
Second, we create two more stacked cubes of the same shape as shown in Figure 2, and form a rectangular prism using the three stacks.
However, we can observe that we cannot form a rectangular prism as shown in Figure 3. A non-square portion of the red cubes are extended to the top face leaving “empty regions.”
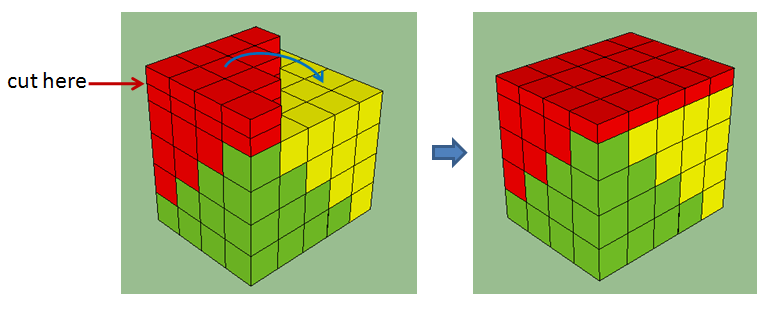
To eliminate the extended area, we cut it into half horizontally, remove half of it, rotate, and fill in the empty regions as shown in the next figure. This makes the final figure a rectangular prism.
We can express its edge lengths of the formed prism in terms of the side length of the largest square prism in each stack which is 4 units. In effect, the dimensions of the prism made of three stacks of cubes are and
. Therefore, the volume is
. However, we have created three stacks, but we only need the volume of one stack, since we are only finding an equivalent expression for the sum of the first four square numbers. So, we divide the volume by 3 making the volume of one stack equal to
.
This process can be generalized to form larger cubes (left as an exercise). In general, the volume of one stack of cubes with whose side length of the largest square is is described by the expression
.
Therefore,
.
Credits
Proof: Man Keung Siu
Reference: Proofs without Words