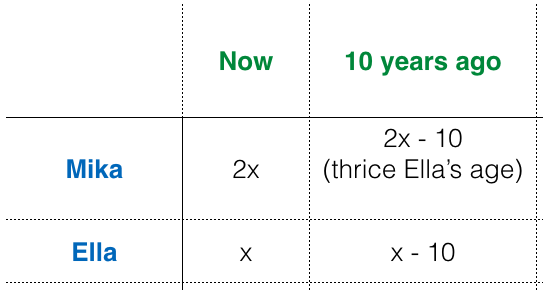Math Word Problems: Solving Age Problems Part 1

This is the second topic in the Word Problems Series. In this series of posts, we are going to discuss age problems.  In age problems, most times, ages of persons at different points in time — past, present, and future — are asked about.

One of the most famous age problems in the history of mathematics is Diohpantus’ Riddle. After this series, you should be able to provide a solution to Diophatus’ age problem. 🙂

As we have done in the previous topic, we will start with simple problems. As we go on, the problems become more complicated.  Let us start with the first problem.

PROBLEM 1

Adrian’s age is one less than twice Carlo’s age. The sum of their ages is 50. What are their ages?

Solution

As you have probably noticed that this problem is very similar to the problems we discussed earlier.  Age problems just like most algebra problems which are number problems in disguise. 

For the solution, let be Carlo’s age. Twice his age is . One less than twice his age is which is Adrian’s age. Since the sum of their ages is , we have

.

Simplifying, we have . This gives us and .

Therefore, Carlo is years old and Adrian is years old.

Note: One common mistake in solving problems containing the word “less” is the confusion between “a less than b” and “a less b.” The expression a less than b is , while the expression a less b is . In the problem above,  the expression 1 less than twice Carlo’s  age is and not .

PROBLEM 2

Maia is three times as old as her daughter. Five years go, the the difference between their ages is . What are their ages?

Solution

In the first sentence,  Maia’s present age is three times as that of her daughter’s age. That means, that if her daughter is years old, then Maia is years old.

Five years ago, Maia and her daughter were five years younger. In effect, years must be subtracted from both their ages. So, 5 years ago, Maia and here daughter’s age were and years respectively.

Now, since the difference of their ages is , we can now set up the equation

.

Solving, we have . This gives us $2x = 26$ or . Therefore, the age of Maia’s daughter is and she is .

PROBLEM 3

Mika is twice as old as Ella. Ten years ago, Mika was three times as old as Ella. What are their present ages?

Solution

Mika is twice as old as Ella, so if Ella is years old, then Mika is . Ten years, ago Ella’s age is and Mika’s age is .

According to the problem, Mika’s age which was was three times   Ella’s age which is . This implies that if we multiply Ella’s age by , their ages will be equal.  That is,

Simplifying, we have

. This gives us . So,

Note: I made the word problems in this series myself, so they were not reviewed. Please inform me if you find the problems confusing.