Understanding the Meaning of Correspondence

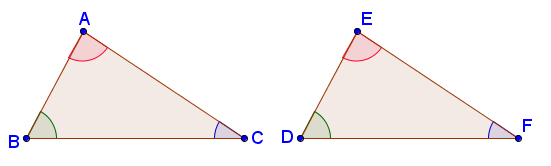
In Geometry, two objects are congruent if they have the same size and shape. Two triangles drawn on a piece of paper are congruent if we can cut them out with scissors, and superimpose them to fit exactly, that is, without gaps or overlaps. If the triangles fit exactly, the corresponding parts are the parts that coincide. Consequently, corresponding parts of congruent triangles are congruent. Therefore, if two triangles are congruent, then their corresponding angles are congruent and their corresponding sides are also congruent.

In the figure above, if we superimpose the two triangles, will coincide with and will coincide with . Hence and are corresponding sides and and are corresponding angles.

Exercise: Name the other corresponding parts of the congruent triangles above.

The double-sided arrow symbol is used to denote correspondence.  We say that angle corresponds to and write . Similarly, we say that corresponds to , and write .

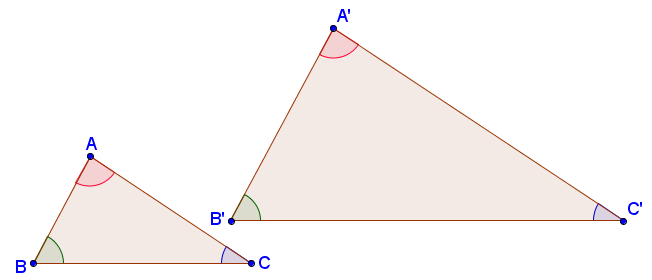
Correspondence is also used in similarity. Two figures are similar, if they are reduced or enlarged proportionally (see details).  In the figure above, triangle is similar to triangle , so and .

Correspondence is an important concept used in different parts of mathematics. For example, in set theory, it can be used to show that the number of negative integers, number of positive integers, and rational numbers are equal.