Math Word Problems: Solving Motion Problems Part 2
This is the second part of the Solving Motion Problems Series, a part of the Math Word Problem Solving Series. In the first part, we have learned that , where
is the distance traveled by an object,
is the rate, and
is the time.
In this post, we discuss the two common types of motion problems: two objects traveling to opposite directions and two objects traveling toward each other.
Problem 1
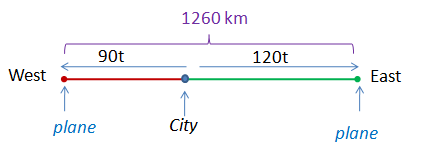
Two trains leave a city at the same time. One train is traveling east at an average speed of 90 kilometers per hour, while the other train is traveling west an average speed of 120 kilometers per hour. In how many hours will they be 1260 kilometers apart?
Solution
Before we proceed with the solution, let us take note of the following. First, the phrase “1260 kilometers apart” means the distance between two trains. Second, the distance between two trains is the sum of the distance traveled by the train traveling west and the distance of the train traveling east. Lastly, the time duration the two trains traveling are equal.
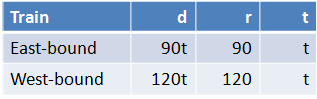
With the facts above, we create the table below. We let be the travel time of each plane (remember, they are equal). Since the distance is the product of the rate and the time, the distances traveled by the east-bound and west-bound train is
and
respectively.
If we add the two distances, the result will be kilometers. Hence,
.
In hours, the two trains will be
kilometers apart.
Check
( km/hr)(
hrs)+(
km/hr)(
hrs)
= km +
km
= km.
Problem 2
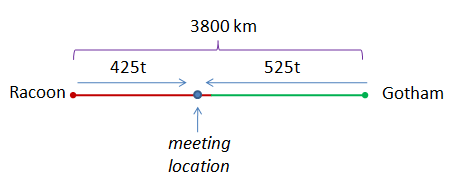
Racoon and Gotham City are 3800 kilometers apart. Plane A leaves Racoon traveling towards Gotham at an average speed of 425 kilometers per hour. Plane B leaves Gothan, the same time, traveling towards Racoon at an average speed of 525 kilometers per hour. When will the two planes meet?
Solution
The second problem is just almost the same as the first problem. The total distance traveled by the two planes is 3800 kilometers by the time they meet. The total distance traveled is equal to the sum of the distances traveled by the two planes.
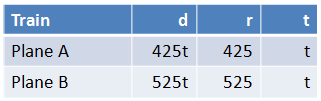
Since distance is equal to the product of the rate and time, the table would look like the figure below.
Therefore, if we add the two distances traveled, we have
.
That means that in four hours, the two planes will meet.
Check
Left as an exercise.
In the next post, we will discuss more motion problems.
—
Photo Credit (Creative Commons): George M. Groutas via Flickr