Finding the Sum of the Arithmetic Sequence

An arithmetic sequence is a sequence of numbers such that the difference between two consecutive terms is constant. The sequence

7, 13, 19, 25, 31, 37, 43, 59

is an example of an arithmetic sequence with first term 7, constant difference 6, and last term 49.

You have learned in that the formula for finding the nth term of the arithmetic sequence $a_n$ with first term $a_1$ , and constant difference $d$ is given by

$a_n = a_1 + (n-1)d$ .

In this post, we derive the formula for finding the sum of all the numbers in an arithmetic sequence. We take the specific example above and use Gauss’ method in finding the sum of the first 100 positive integers. Recall that in adding the first 100 integers, Gauss added the first integer to the last, the second integer to the second to the last, the third integer and the third to the last and so on.

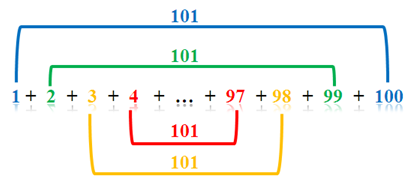
Sum of Arithmetic Sequence

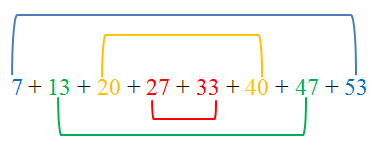
As we can see, this strategy can be applied to the given above. If we add the 1st and the 8th term, the 2nd and the 7th term, and so on, the sums are the same. Observe that the sequences has 8 terms and we have 8/2 = 4 pairs of numbers with sum 60.

Now, how do we generalize this observation?

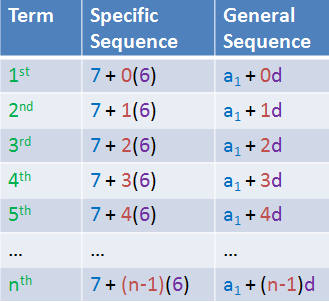
First notice that to get the terms in the sequence, the multiples of the constant difference is added to the first term. For example, to get the second term, we have 7 + (1) 6, and to get the third term, we have 7 + 2(6). Continuing this pattern, we can see the complete terms the second column in the table below. Their generalized form are shown in the third column.

If we use Gauss’ strategy in finding the sum of the generalized arithmetic sequence, $a_1$ pairs with $a_1 + (n-1)d$ , $a_2$ will pair with $a_1 + (n - 2)d$ , and so on. If we add each pair, the sum is always

$2a_1 + (n - 1)d$ .

But we have $n$ terms in the sequence which means that there are $\frac{n}{2}$ pairs. Therefore, the sum $S$ of the generalized arithmetic sequence is given by the formula

$S = \displaystyle\frac{n}{2}[(2a_1 + (n-1)d]$ .

Take note that the preceding formula can be expanded to $S = \frac{n}{2}[a_1 + a_1 + (n - 1)d]$ . But since $a_n = a_1 + (n-1)d$ ,

$S = \frac{n}{2}(a_1 + a_n)$ .

Consequently, it is easy to get the sum of an arithmetic sequence from $a_1$ up to $a_n$ , if both of them are given.

4 comments on “Finding the Sum of the Arithmetic Sequence”

MathyNick on February 5, 2013 at 7:51 pm said:

I think the sequence you were going for is:
7, 13, 19, 25, 31, 37, 43, 49.

It’s a neat coincidence that each term adds up to 60 with the posted sequence but the difference between each consecutive term is not a constant difference of 6:
53 – 47 = 6
47 – 40 = 7
40 – 33 = 7
33 – 27 = 6
27 – 20 = 7
20 – 13 = 7
13 – 7 = 6

Reply ↓

Guillermo Bautista on February 6, 2013 at 4:48 am said:

Thanks Nick. I can’t believe I didn’t see that. I’m probably getting old. I changed it already.

Reply ↓

MathyNick on February 6, 2013 at 8:47 am said:

These are some other changes you’ll may want to consider:

Update this image:
http://mathandmultimedia.com/wp-content/uploads/2013/02/sum-arithmetic-sequence.png

“As we can see, this strategy can be applied to the given above. If we add the 1st and the 8th term, the 2nd and the 7th term, and so on, the sums are the same. Observe that the sequences has 8 terms and we have 8/2 = 4 pairs of numbers with sum ***56***.”

“First notice that to get the terms in the sequence, the multiples of the constant difference is added to the first term. For example, to get the second term, we have 7 + (1) 6, and to get the ***third*** term, we have 7 + 2(6).”

This is optional:
For additional clarity, I would add “(the last term)” somewhere in “a_1 pairs with a_1 + (n-1)d,” and (the second-to-last term)” somewhere in ” a_2 will pair with a_1 + (n-2)d” so the reader can understand what term you’re referencing within Gauss’s method.

I hope these suggestions help and don’t sound annoying.

~Nick

Reply ↓

Guillermo Bautista on February 6, 2013 at 10:32 am said:

Thank you very much Nick. No, it’s not annoying, it’s very helpful. I really appreciate your time in reading and making valuable comments. I will update the post as soon as possible.

Your comments are most welcome.

Reply ↓